2.1 Regla de la Cadena y Composición de Funciones
Esta es la regla más importante y que nos permitirá derivar cualquier tipo de función. f ( x ) = sin ( a x + b ) es una composición de las funciones elementales g ( x ) = sin y h ( x ) = a x + b
Ejemplo:
es una composición de las funciones elementales.
y
La composición de funciones nos dice que o, en otra notación, . Podríamos lógicamente hacer composiciones de tres funciones distintas, o de cuatro, o de cuantas funciones queramos.
 Regla de la Cadena
La regla de la cadena nos proporciona la derivada de la composición de funciones:
Regla de la Cadena
La regla de la cadena nos proporciona la derivada de la composición de funciones:
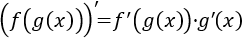 Explicamos las reglas de derivación y la regla de la cadena para el cálculo de derivadas. Ejercicios resueltos de calcular derivadas.
Es más fácil de entender mediante ejemplos.
Ejemplo 1:
Explicamos las reglas de derivación y la regla de la cadena para el cálculo de derivadas. Ejercicios resueltos de calcular derivadas.
Es más fácil de entender mediante ejemplos.
Ejemplo 1:
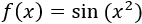 Se trata de la composición de la función seno y la funciónn cuadrado. Su derivada es la derivada del seno por la derivada del cuadrado:
Se trata de la composición de la función seno y la funciónn cuadrado. Su derivada es la derivada del seno por la derivada del cuadrado:
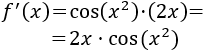 Ejemplo 2:
Ejemplo 2:
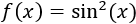 Tenemos las mismas funciones, pero con el orden de composición intercambiado. Su derivada es la derivada del cuadrado por la del seno:
Tenemos las mismas funciones, pero con el orden de composición intercambiado. Su derivada es la derivada del cuadrado por la del seno:
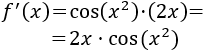 Ejemplo 3:
Ejemplo 3:
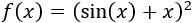 Para derivar esta función tenemos que aplicar la regla de la cadena y la regla de derivación de la suma de funciones:
Para derivar esta función tenemos que aplicar la regla de la cadena y la regla de derivación de la suma de funciones:
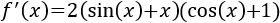 Composición de las Funciones
La composición de funciones es la imagen resultado de la aplicación sucesiva de dos o más funciones sobre un mismo elemento x. La composición de funciones se realiza aplicando dichas funciones en orden de derecha a izquierda, de manera que en (g o f)(x) primero actúa la función f y luego la g sobre f(x).
Composición de las Funciones
La composición de funciones es la imagen resultado de la aplicación sucesiva de dos o más funciones sobre un mismo elemento x. La composición de funciones se realiza aplicando dichas funciones en orden de derecha a izquierda, de manera que en (g o f)(x) primero actúa la función f y luego la g sobre f(x).
 Ejemplo:
Del gráfico adjunto determinar F o G
Ejemplo:
Del gráfico adjunto determinar F o G
 Se consideran sólo los elementos asociados a líneas que hacen el recorrido completo de A hacia C, pasando por B.
FoG= {(2; 7), (3;7), (0;8)}
Video Explicativo:
https://www.youtube.com/watch?v=m_5-WS9Nd68
Se consideran sólo los elementos asociados a líneas que hacen el recorrido completo de A hacia C, pasando por B.
FoG= {(2; 7), (3;7), (0;8)}
Video Explicativo:
https://www.youtube.com/watch?v=m_5-WS9Nd68
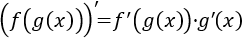 Explicamos las reglas de derivación y la regla de la cadena para el cálculo de derivadas. Ejercicios resueltos de calcular derivadas.
Es más fácil de entender mediante ejemplos.
Ejemplo 1:
Explicamos las reglas de derivación y la regla de la cadena para el cálculo de derivadas. Ejercicios resueltos de calcular derivadas.
Es más fácil de entender mediante ejemplos.
Ejemplo 1:
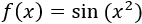 Se trata de la composición de la función seno y la funciónn cuadrado. Su derivada es la derivada del seno por la derivada del cuadrado:
Se trata de la composición de la función seno y la funciónn cuadrado. Su derivada es la derivada del seno por la derivada del cuadrado:
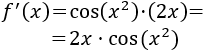 Ejemplo 2:
Ejemplo 2:
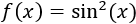 Tenemos las mismas funciones, pero con el orden de composición intercambiado. Su derivada es la derivada del cuadrado por la del seno:
Tenemos las mismas funciones, pero con el orden de composición intercambiado. Su derivada es la derivada del cuadrado por la del seno:
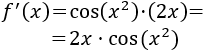 Ejemplo 3:
Ejemplo 3:
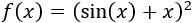 Para derivar esta función tenemos que aplicar la regla de la cadena y la regla de derivación de la suma de funciones:
Para derivar esta función tenemos que aplicar la regla de la cadena y la regla de derivación de la suma de funciones:
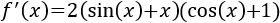 Composición de las Funciones
La composición de funciones es la imagen resultado de la aplicación sucesiva de dos o más funciones sobre un mismo elemento x. La composición de funciones se realiza aplicando dichas funciones en orden de derecha a izquierda, de manera que en (g o f)(x) primero actúa la función f y luego la g sobre f(x).
Composición de las Funciones
La composición de funciones es la imagen resultado de la aplicación sucesiva de dos o más funciones sobre un mismo elemento x. La composición de funciones se realiza aplicando dichas funciones en orden de derecha a izquierda, de manera que en (g o f)(x) primero actúa la función f y luego la g sobre f(x).
 Ejemplo:
Del gráfico adjunto determinar F o G
Ejemplo:
Del gráfico adjunto determinar F o G