Función circunferencia.
Para empezar vamos a conocer la función con la que trabajaremos en los primeros ejercicios.
¿Existe una función cuya gráfica sea una circunferencia?
La respuesta es no.
Como se aprecia a continuación, si consideramos que una circunferencia es la gráfica de cierta función encontraremos valores del dominio que tienen más de una imagen, cosa que contradice la definición de función.
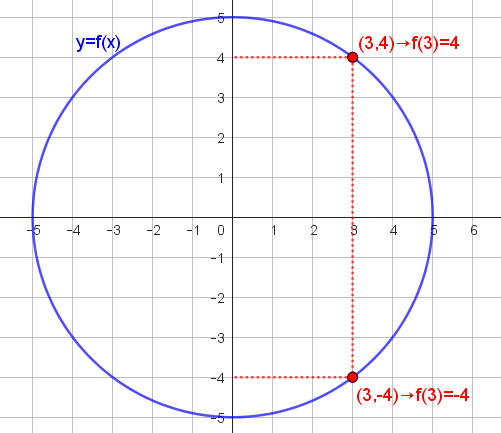
¿Cuál es la imagen de 3?... ¿4 o -4?
Por lo tanto no hay una función cuya gráfica sea una circunferencia. Sin embargo sí podemos encontrar dos funciones tales que la unión de sus gráficas formen una circunferencia. Una de ellas sería la semicircunferencia positiva del ejemplo anterior, y la otra la negativa.
No es difícil expresar analíticamente la coordenada "y" de un punto cualquiera de una circunferencia en función de la coordenada "x" y del radio de la misma. Solo hay que observar que las longitudes de las coordenadas de cada punto de la circunferencia, junto con el radio forman un triángulo rectángulo y por lo tanto verifican el Teorema de Pitágoras:
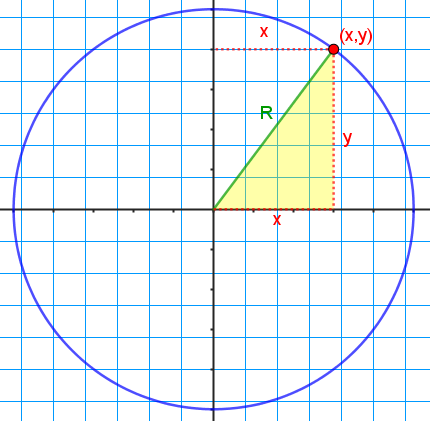
Aplicando el Teorema de Pitágoras:
y despejando
Así tenemos las dos expresiones de las dos funciones cuyas graficas forman una circunferencia.
Para el caso de una circunferencia de radio 1 (R=1) quedarías así:
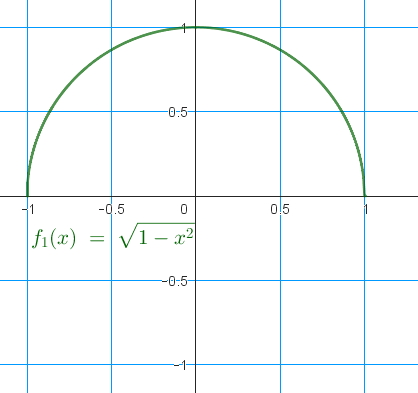
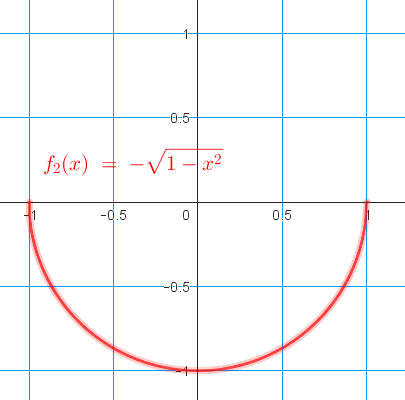
En el ejercicio que proponemos a continuación trabajaremos solo con una de las dos funciones (la positiva) que directamente llamaremos f(x).