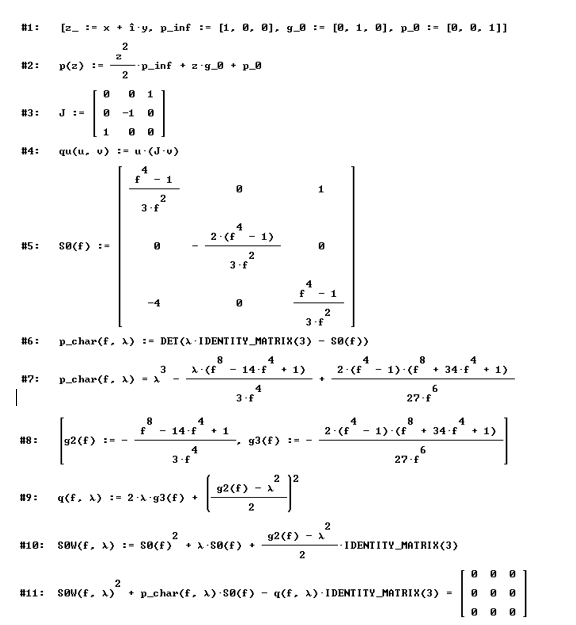
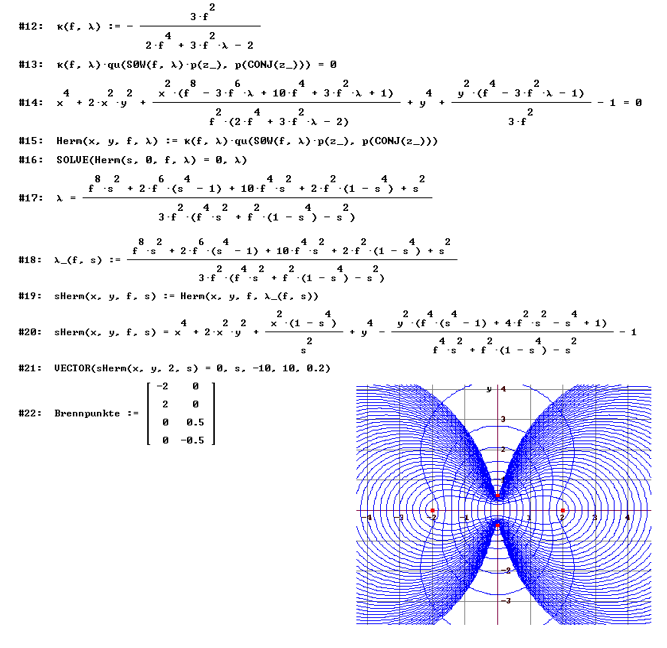
1-teilige Quartik: Gleichungen
Diese Seite ist Teil des GeoGebra-Books Moebiusebene.
Nachtrag (28.04.2021) und Vereinfachung der Formeln: siehe unten
Die Gleichung der oben angezeigten bizirkularen Quartik lautet:
- für , also
(*)
oder , wobei
invariant unter Spiegelungen an der - und an der -Achse ist.
Die Gleichung des Leitkreises für den Brennpunkt und lautet:Die Quartik ist eine der konfokalen bizirkularen Quartiken mit den Brennpunkten .
Rechnerische Begründung mit Hermitescher Wurzel des zugehörigen quadratischen Vektorfeldes.
In Geradenkoordinaten (siehe oben das Hilfefenster "Euklidisches KOS") gilt für die Verbindungsgeraden und .
Eine der beiden Geraden wird als elliptisches, das andere als hyperbolisches Kreisbüschel gewählt.
Die Kreise sind dann orthogonal zu einer der beiden Achsen; und die im folgenden zu berechnenden
selbstadjungierten Matrizen besitzen reelle Koeffizienten, was Voraussetzung für die Bildung Hermitescher Formen ist.
Die folgende symmetrische Bilinearform definiert eine bezüglich selbstadjungierte Abbldung :
mit der Matrix . Auf der Möbiusquadrik ist durch
ein quadratisches Vektorfeld gegeben, welches für alle dasselbe ist.
Wir wählen aus dieser Schar diejenige selbstadjungierte Abbildung , für die ist.
Wir berechnen das charakteristische Polynom von :
- mit reellen und . (Konkrete Werte s. u.!)
Damit kann man die "Wurzeln" von erklären: .
Man rechnet nach: mit einer reellwertigen Funktion (s.u.).
Für eine mit , und damit auch mit vertauschbare Spiegelung in , d.h. eine involutorische
Hermitesche Abbildung, ist dann eine Hermitesche Wurzel von .
Mit vertauschbare Spiegelungen sind die Spiegelung an der -Achse und die Spiegelung an der -Achse.
Die Spiegelung an der -Achse ist schnell erklärt: ,
insbesondere gilt im Geradenraum auf der Möbiusquadrik: .
Damit können wir die Lösungskurven des quadratischen Vektorfeldes berechnen:
mit einem reellwertigem, von Null verschiedenem Faktor .
Um die Scheitel auf der -Achse zu ermitteln, setzen wir in die Gleichung ein und erhalten:
Setzt man dieses von abhängige in die Hermitesche Gleichung ein,
so erhält man die oben angegebene Quartik-Gleichung (*).
Die Rechnungen im Einzelnen wurden mit der "veralteten" CAS-Software DERIVE durchgeführt.
Damit ist es möglich, problemlos mit komplexen Vektoren und Matrizen zu rechnen.
Vektoren und Matrizen werden einheitlich als Listen geführt.
Funktionen und Abbildungen können problemlos ohne Spezifizierung der Variablen definiert und verarbeitet werden.
Auch eine größere Anzahl von impliziten Funktionen werden sekundenschnell exakt berechnet
(mit Brüchen und Wurzeln, falls die Eingaben rational waren) und ebenso schnell gezeichnet. Siehe die Ausschnitte unten.
Nachtrag 28.04.2021: die Formeln
Eine 1-teilige bizirkulare Quartik besitzt in Normalform die Gleichung:
In dieser Normal-Gleichung ist die Symmetrie bezüglich der Koordinaten-Achsen, und, wie wir sehen werden,
(*) die Lage der Brennpunkte mit verarbeitet.
- Mit berechnet man die -Achsenschnittpunkte und
entsprechend die -Achsenschnittpunkte als komplexe Punkte in .
- Mit berechnet man die 4 Brennpunkte, siehe (*)
Bemerkung: Im Handbuch von geogebra wird zwar bemerkt, dass geogebra komplexe Zahlen nicht unterstützt;
dennoch rechnet geogebra trefflich sowohl die Rechenvorschriften als auch die Funktionen komplex, wenn man die angegebenen Tricks verwendet.
Konfokale bizirkulare Quartiken besitzen (per definitionem) dieselben Brennpunkte und damit dasselbe
oben berechnete . Festgelegt sind sie durch die Scheitelpunkte auf der -Achse.
Die Koeffizienten der konfokalen Quartiken ermittelt man daher mit den Formeln:
Man vergleiche hierzu auch die Seite: Darboux Cycliden: die Formeln 2