Atividade Razão e Proporção
Razão e proporção
- Em medicina, a precisão nos cálculos de razão e proporção é vital para determinar as doses corretas de medicamentos a serem administradas aos pacientes. Uma dosagem incorreta pode resultar em efeitos colaterais indesejados ou até mesmo colocar em risco a vida do paciente. Além disso, a administração precisa de medicamentos é crucial para garantir que o tratamento seja eficaz.
- Na engenharia e na construção, os cálculos de razão e proporção são usados para dimensionar estruturas, calcular materiais necessários e garantir a estabilidade e segurança das construções. Erros nesses cálculos podem levar a falhas estruturais graves e colocar em risco a vida das pessoas que utilizam essas estruturas.
- Na agricultura, o uso correto de cálculos de razão e proporção é fundamental para determinar a quantidade de insumos, como fertilizantes e defensivos agrícolas, a serem aplicados em uma determinada área de cultivo. Isso afeta diretamente a produtividade das colheitas e a saúde do solo, além de minimizar o desperdício de recursos.
- Na culinária e na preparação de receitas, os cálculos de razão e proporção garantem que os ingredientes sejam combinados na quantidade certa, resultando em pratos saborosos e bem-sucedidos. Além disso, em receitas que exigem conversões de medidas, como gramas para xícaras ou litros para mililitros, os cálculos precisos são essenciais para obter resultados consistentes.
1) Encontre o valor adequado para a proporção:
Observe a imagem 1 e responda! Justifique como encontrou!
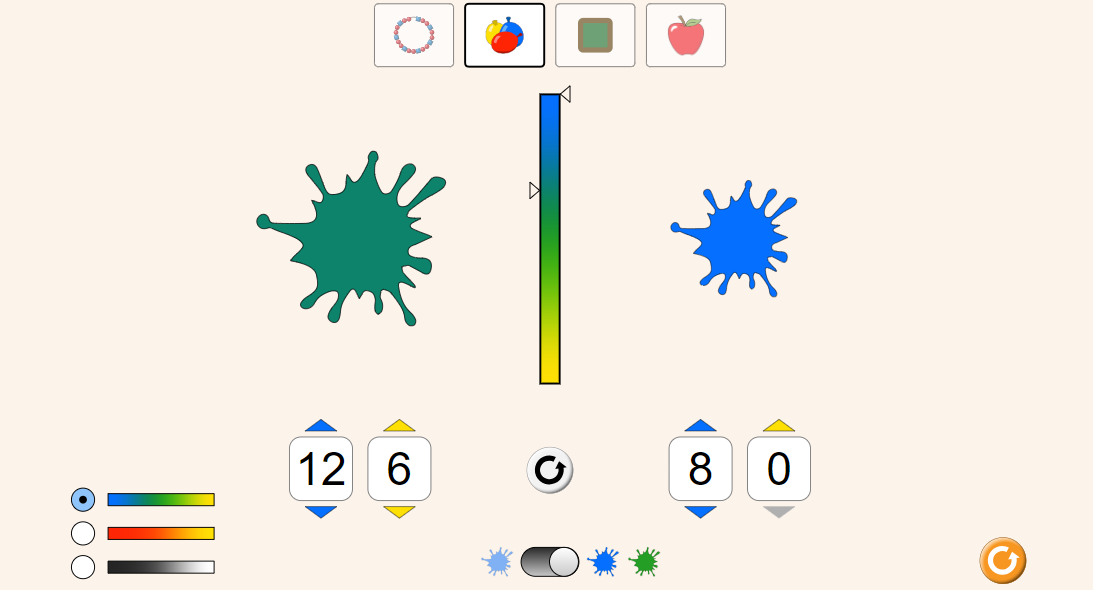
2) Para cada imagem abaixo encontre o valor apropriado:
Qual valor devemos substituir o "0" para obter a taxa de proporção correta?
a)
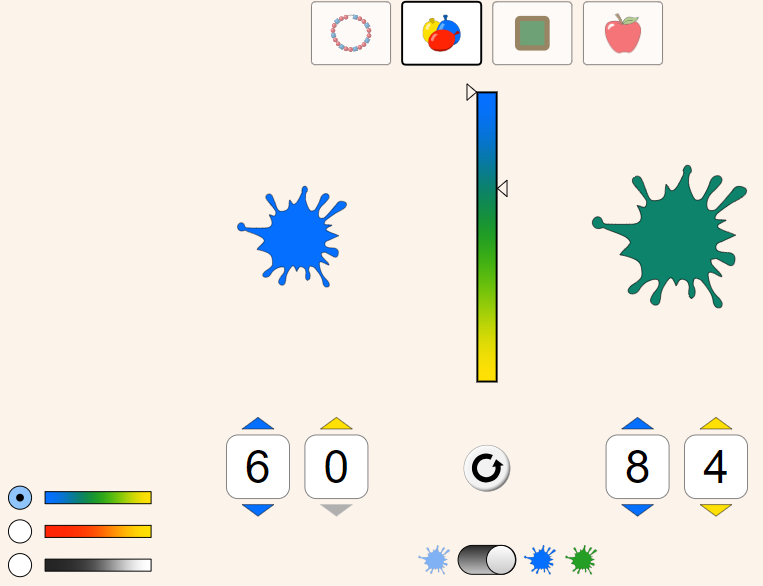
b)
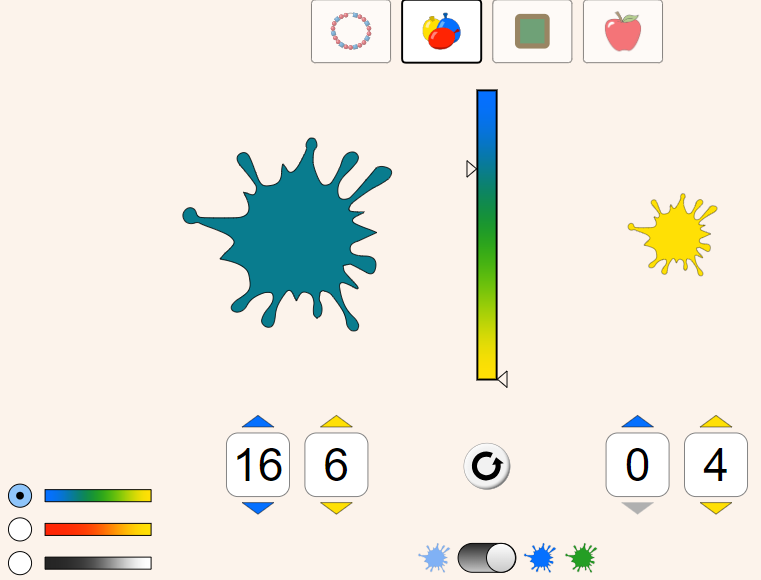
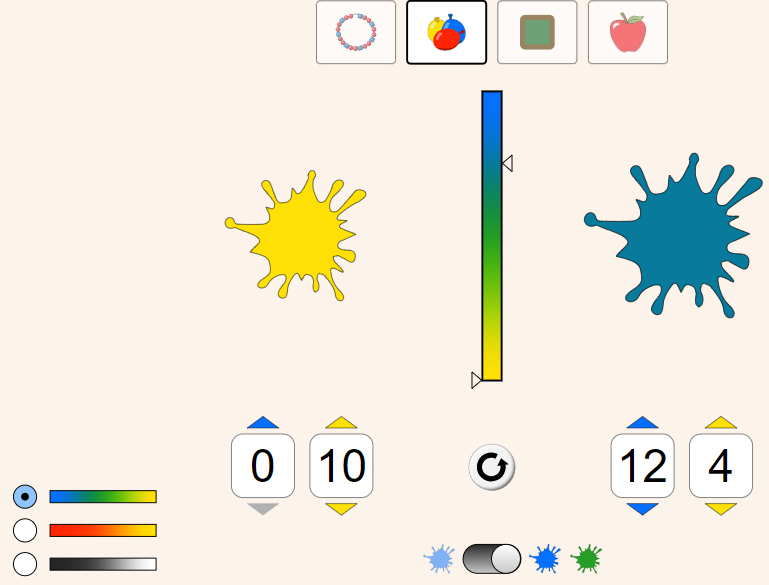
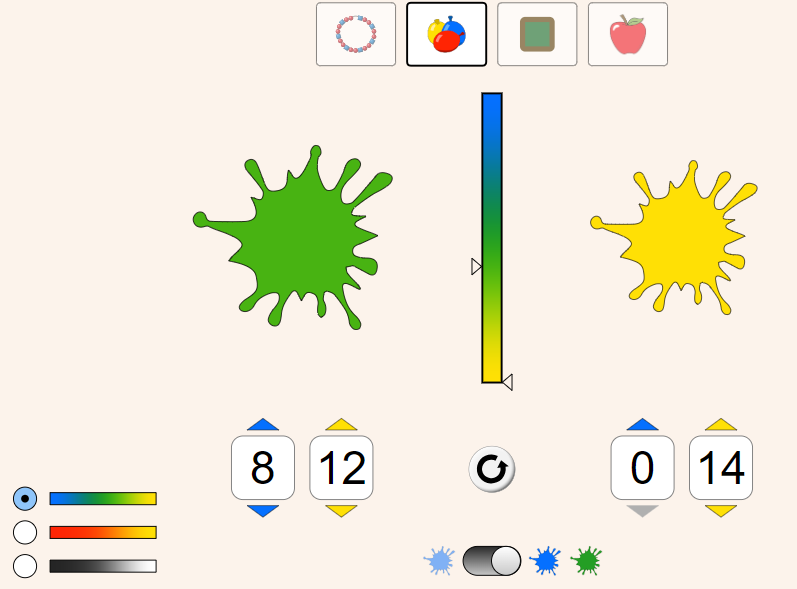
Verifique no simulador acessando abaixo:
3 - (UFOP-MG–2008)
(UFOP-MG–2008) Duas torneiras são utilizadas para encher um tanque vazio. Sabendo que sozinhas elas levam 10 horas e 15 horas, respectivamente, para enchê-lo. Quanto tempo às duas torneiras juntas levam para encher o tanque? Atenção: Às duas torneiras juntas encherão o tanque com uma velocidade v1,2 = v1 + v2!
4) Exercício para desenvolver Álgebra
Encontre o valor das incógnitas das proporções a seguir, de tal forma que elas sejam verdadeiras. a) x/3 = 24/6 b) 4/y = 20/3 c) 11/2 = 2/z
Medida e razão de segmentos
5) Anote a relação dos segmentos em relação a unidade estabelecida:
6) Agora com a relação da unidade e sua metade:
Observe a relação entre as medidas
Observe a relação dos segmentos laterais e a Área das figuras:
Aplicação de razão e proporção entre segmentos

7) Relação entre segmentos e sua aplicações: (não discutiremos os princípios físicos apenas a relação direta da aplicação, observe a imagem abaixo)
(ITA-SP) Para medir a febre de pacientes, um estudante de medicina criou sua própria escala linear de temperaturas. Nessa nova escala, os valores de O (zero) e 10 (dez) correspondem, respectivamente, a 37°C e 40°C. A temperatura de mesmo valor numérico em ambas as escalas é aproximadamente:
relação da escala
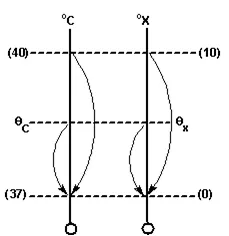
DESAFIO!
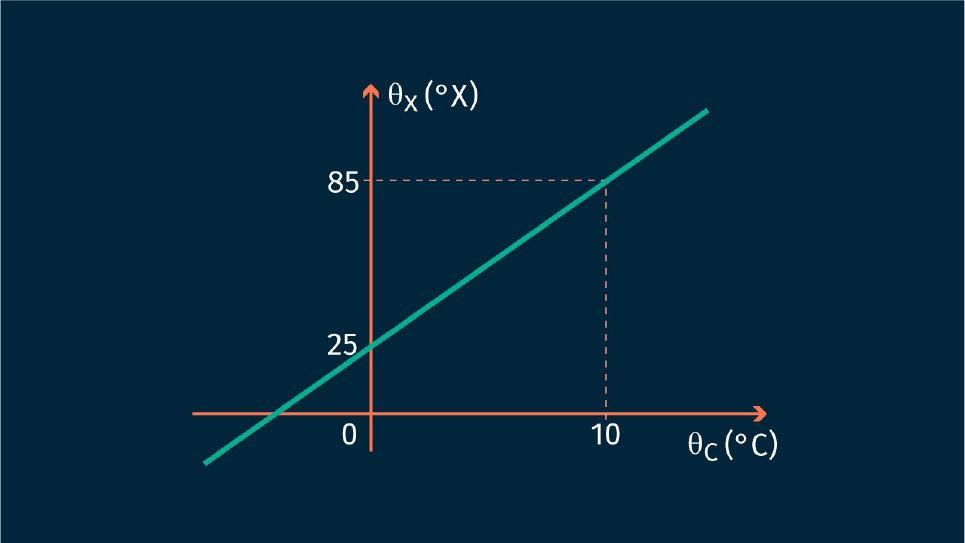
Você atua em uma fábrica de cervejas que utiliza a calorimetria para sua produção. Durante a fermentação, as leveduras irão consumir os açúcares fermentáveis do mosto gerando o álcool e o CO2, os aromas e sabores, e também a redução do pH da cerveja. O tempo e a temperatura de fermentação podem variar de acordo com a densidade inicial do mosto, o tipo de levedura utilizado e as características que você busca na cerveja. Em um composto são misturados 100g de água líquida a 20 °C com 200g de um acidulante a 75°C. Uma tabela informa que o calor específico da água líquida e do acidulante é onde X é uma escala arbitrária de temperatura, cuja relação com a escala Celsius está representada no gráfico. Obtenha uma equação de conversão entre as escalas X e Celsius e, considerando que a mistura seja feita dentro de um calorímetro ideal, calcule a temperatura final da mistura, na escala Celsius, depois de atingido o equilíbrio térmico. No exercício não discutiremos os princípios físicos mas sim a relação da escala com o tópico de razão entre segmentos:
gráfico da escala