Integralrechnung
1. Integralrechnung in der Schule
1.1 Integrale in der Oberstufe
Die Integralrechnung ist ein Oberstufenthema und findet sich in dem entsprechenden Bildungsplan wieder. Wichtig ist dabei, dass wir hier die Leitideen „Funktionaler Zusammenhang“, „Zahl-Variable-Operation“ und „Messen“ betrachten.
Durch den Funktionalen Zusammenhang sollen SuS die Werkzeuge der Integralrechnung nutzen und einsetzten können.
Weiter schult Zahl-Variable- Operation das Aufsummieren von Flächen.
Letztlich ist der Fokus von Messen die Berechnung von Flächeninhalte/Volumen und deren graphischen Deutung.
1.2. Aspekte und Grundvorstellungen der Integralrechnung
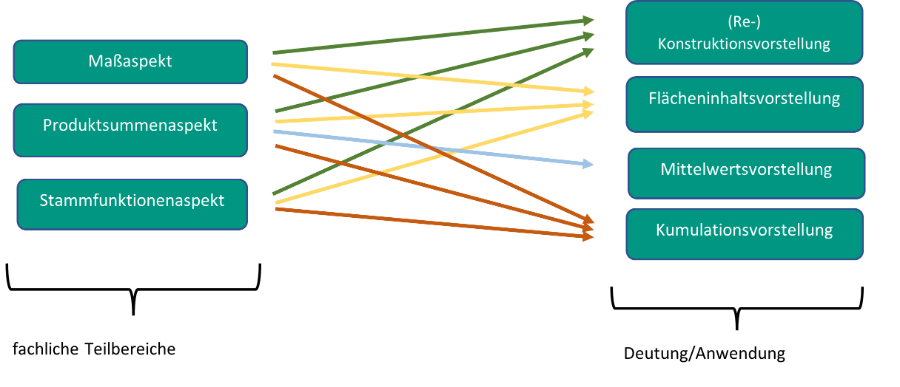
Wie im Schaubild zu sehen, sind die Aspekte mit den Grundvorstellungen verbunden. Dies sorgt für eine Brücke zwischen den fachlichen Teilbereichen und den Deutungen hinter der Integralrechnung. So vernetzten wir nicht nur die Werkzeuge, sondern beispielsweise die grafischen Vorstellungen. Betrachten wir im Folgenden die Grundvorstellungen.
(Re-)Konstruktionsvorstellung setzt sich zusammen aus:
1. (Re‐)konstruiert einer Größe aus ihrer Änderungsrate.
Beispiel: Badewanne einlassen, Luftvolumen,…
2. (Re‐)konstruiert eine Fläche
Beispiel: GeoGebra-Aktivität "Zusammenhang zwischen F(x) und f(x).
Beispiel für Zusammenhang zwischen F(x) und f(x).
Durch das bewegen von A auf F(x) sieht man wie sich P auf f(x) verhält.
Anhand dieser beiden Grafiken kann man etwa verdeutlichen, dass die Nullstelle von f(x) die Extremstellen von F(x) sind.
Flächeninhaltsvorstellung setzt sich zusammen aus:
1.Berechnen des Flächeninhalts
Nicht negativ
Graph verläuft oberhalb, unterhalb oder schneidet die x-Achse
2. Bestimmtes Integral als Bilanz von Flächeninhalten
Orientierter Flächeninhalt
Negative Ergebnisse oder Nullwerte möglich
Mittelwertsvorstellung setzt sich zusammen aus:
1. Ein bestimmtes Integral mittelt eine Größe
Kumulationsvorstellung setzt sich zusammen aus:
1. Aufsummieren kleinerer Summanden mit Produktstruktur
2. Grenzwert einer Summe von Rechtecksflächen
Bsp: Ober-/Untersumme
Beispiel für Ober-/Untersumme
2. Doppelte Diskontinuität
Die doppelte Diskontinuität beschreibt den Übergang von Schule zu Universität und zurück.
Die erste Diskontinuität definiert dabei den Wechsel von Schüler:in zu Studierenden.
Für Lehramtsstudierende ist noch die zweite Diskontinuität von Bedeutung. Denn
schließlich werden diese von der Universität wieder zurück zur Schule gehen, um
dort zu unterrichten.
2.1. Erste Diskontinuität
Eine Besonderheit in der Literatur zeigt sich schnell in dem Fach Mathematik. Durch verschiedene Sichtweisen auf die Mathematik in der Schule und in der Universität können sich Studienanfänger:innen schnell überfordert fühlen. Diese werden im nachfolgenden kurz beleuchtet.
a) Bildungsziel
In der Schule:
-Allgemeinbildung
-Neben dem Fachwissen auch den Bildungsauftrag
-Persönlichkeitsbildung, ….
In der Universität
-Spezialbildung
-Fachliche Ausbildung
- Wissensansammlung
b) Axiomatik
In der Schule
-„Weiche“ Axiomatik
-Leichte Beweisführungen
-Lockerer Aufbau von „Definition-Satz-Beweis“
In der Universität
-„Strenge“ Axiomatik
- Starker Fokus auf korrekte Ausführung
- Viele Beweisformen
- Aufbau nach dem Prinzip „Definition-Satz-Lemma-Korolla-Beweis“
Neben diesen drei Aspekten kann man noch die Sprache, den Realitätsbezug, Anforderungsbereiche, das Lerntempo und ähnliches betrachten.
Durch die verschieden Sichtweisen der Mathematik in Schule und Universität ist neben dem mathematischen Verständnis auch eine feste Struktur wichtig. Dies sollte man bei SuS fördern.
2.2. Zweite Diskontinuität
Für Lehramtsstudierende kommt es bei dem Übergang von Universität zur Schule erneuet zu Hürden, welche in der Literatur durch die zweite Diskontinuität beschrieben ist.
Es kommt zum Zwiespalt zwischen dem fachlichen Fundament, was man sich aneignet und der pädagogischen Handlung dahinter. Und zeitgleich, wie man mit dem erreichten Wissen seinen Unterricht
absichern kann. Es stellt sich unweigerlich die Frage, ob man jetzt Wissenschaftler:in ist oder doch
Pädagog:in?
Dabei ist zu berücksichtigen, dass man darüber reflektiert, inwiefern man sein Fachwissen in den Unterricht
einfließen lässt. Dies ist etwa beiden Punkt 1.2. zu sehen, wo die Aspekte und
Grundvorstellungen zusammenspielen.
Abschließend lässt sich sagen, dass durch unser fachliches Wissen, wie etwa in der Integralrechnung, unser Unterricht abgesichert werden kann. Durch Aspekte und Grundvorstellungen können wir die pädagogische und fachwissenschaftliche Seite vereinbaren. Anlässlich der Digitalisierung eröffnen sich neue Möglichkeiten in der Nachhilfe. Diese können wir für unsere SuS nutzen und selbst durch das große Angebt an Lernvideos und Co. profitieren.
Literatur
Arens, Hettlich, Karpfinger, Kockelkorn, Lichtenegger, Stachel. Mathematik. S. 415/416. Springer Spektrum.
Baden-Württemberg Mathematik. Bildungsplan. http://www.bildungsplaene-bw.de/site/bildungsplan/get/documents/lsbw/export-pdf/depot-pdf/ALLG/BP2016BW_ALLG_GYM_M.pdf (15.01.2023)
Blum-Barkmin. Diskontinuität in der Linearen Algebra und ein Höherer Standpunkt. Qualitative Untersuchungen in verschiedenen berufsbiografischen Abschnitten und Konkretisierung einer Denkfigur. Springer Spektrum.
Greefrath, Oldenburg, Siller, Ulm, Weigand. Didaktik der Analysis. Springer.
Halverscheid, Kersten, Schmidt-Thieme. Bedarfsgerechte fachmathematische Lehramtsausbildung. Analyse, Zielsetzungen
und Konzepte unter heterogenen Voraussetzungen. Springer Spektrum.