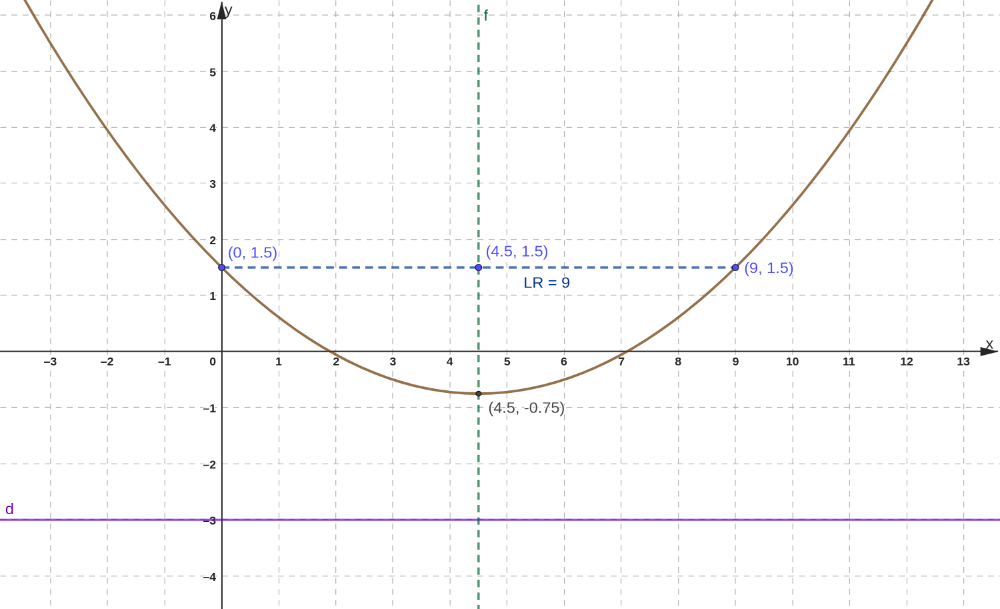
Parábolas com vértice V=(h,k)
Parábola
Sejam, um plano associado a um sistema de coordenadas cartesianas, um ponto e uma reta , denomina-se parábola o lugar geométrico dos pontos , tais que .
Parábola vertical com vértice V=(h,k)
Sejam, , e constantes reais, com diferente de zero, um ponto e uma reta horizontal de equação , a parábola é o lugar geométrico dos pontos tais que .
Para determinar a equação da parábola , calculamos a equação .
e
Portanto a equação buscada é com
Elementos
1 - Parâmetro ;
2 - Vértice ;
3 - Foco ;
4 - Diretriz, reta horizontal de equação ;
5 - Eixo focal ou eixo de simetria, reta vertical de equação ;
6 - Latus rectum ;
7 - Lugar geométrico dos pontos tais que com .
Condições
Se a parábola tem concavidade voltada para cima;
Se a parábola tem concavidade voltada para baixo.
Observação sobre as equações
A equação da parábola vertical com é chamada de equação reduzida, ou equação na forma reduzida. Quando desenvolve-se a equação reduzida, obtém-se uma equação da forma com , tal equação é dita equação geral, ou equação na forma geral.
Parábola Vertical com vértice V=(h,k)
Parábola horizontal com vértice V=(h,k)
Sejam , e , constantes reais com , um ponto uma reta vertical de equação , a parábola é o lugar geométrico dos pontos tais que .
Para determinar a equação de , calculamos a equação
e
.
Portanto a equação buscada é com
Elementos
1 - Parâmetro ;
2 - Vértice ;
3 - Foco ;
4 - Diretriz, reta vertical de equação ;
5 - Eixo Focal, ou eixo de simetria é reta horizontal de equação
6 - Latus rectum ;
7 - Lugar geométrico dos pontos tais que com .
Condições
Se a parábola tem concavidade voltada para a direita.
Se a parábola tem concavidade voltada para a esquerda.
Observação sobre as equações
A equação da parábola vertical com é chamada de equação reduzida, ou equação na forma reduzida. Quando desenvolve-se a equação reduzida, obtém-se uma equação da forma com , tal equação é dita equação geral, ou equação na forma geral.
A equação geral da parábola e o método de Completar quadrados
Como visto, do estudo da equação reduzida de uma parábola, é possível deduzir seus elementos e do seu desenvolvimento, obtém-se a equação na forma geral, ou seja, dada a equação na forma reduzida de uma parábola obtém-se a equação na forma geral. Por outro lado, dada a equação na forma geral de uma parábola, as informações sobre seus elementos não são deduzidas de forma imediata, para tanto, deve-se reescrevê-la na forma reduzida.
A questão é: Como reescrever a equação de uma parábola da forma geral para a forma reduzida?
Para reescrever a equação geral de modo a obter a equação reduzida de uma parábola aplica-se o método de completar quadrados.
O método de completar quadrados
Um dos métodos mais antigos de resolver uma equação do segundo grau, é o método de Completar quadrado, seu desenvolvimento é atribuído ao matemático árabe al-Khwarizmi (750 a 850 d.C.), considerado o patrono da álgebra. Nas equações a incógnita ele chamava "coisa", a ele também é atribuído a utilização da letra "x" para representá-la.
Antes de tratar do desenvolvimento do método de completar quadrados, considere o produto notável quadrado da soma de dois termos
que pode ser expressado como um algoritmo "o quadrado do primeiro termo, mais duas vezes o primeiro pelo segundo, mais o quadrado do segundo". Ou o produto notável quadrado da diferença entre dois termos.
Equações do segundo grau, que possuem a forma desenvolvida de um destes produtos notáveis, podem representar a área de regiões quadradas e são conhecidos como trinômio quadrado perfeito.
Observe as Figuras 01 e 02, ambas representam uma região quadrada.
O quadrado da Figura 01, por exemplo, é composto por
1 - um quadrado azul, cujo lado tem medida desconhecida, representaremos o lado do quadrado por e a região azul é dada por ;
2 - dois retângulos verdes, cada um com um lado de medida e o outro de medida , e sua região é dada por , como são dois retângulos, a região verde tem medida ;
3 - e um quadrado amarelo de lado unitário, cuja região é dada por .
Ou seja, pela soma das regiões obtém-se a área A do quadrado, ou seja .
Observe ainda que o lado do quadrado tem medida , ou seja a área A, pode ser obtida pelo seguinte desenvolvimento
ou seja, uma região quadrada representada por uma equação do segundo grau, da forma trinômio quadrado perfeito.
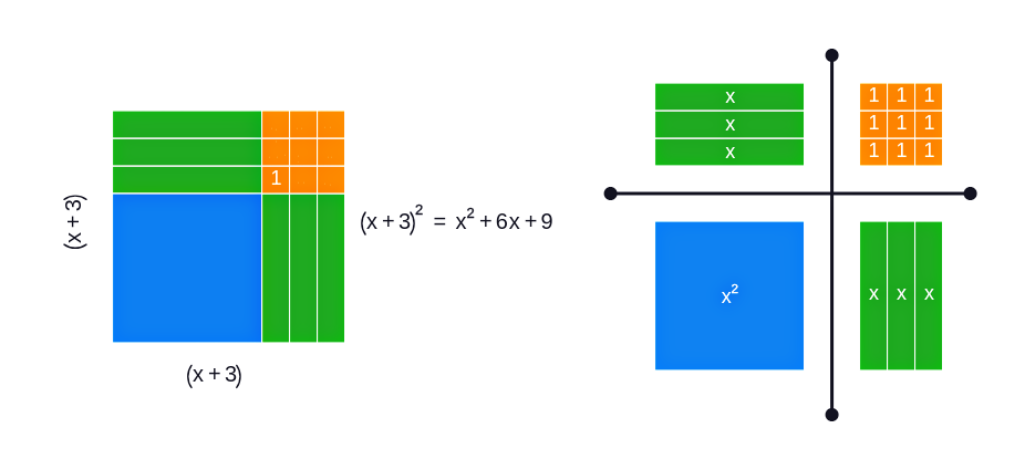
De forma análoga, a área A do quadrado da Figura 02, pode se obtida da seguinte forma
.
Figura 01: Representação de um quadrado de Área: (x+1)(x+1)
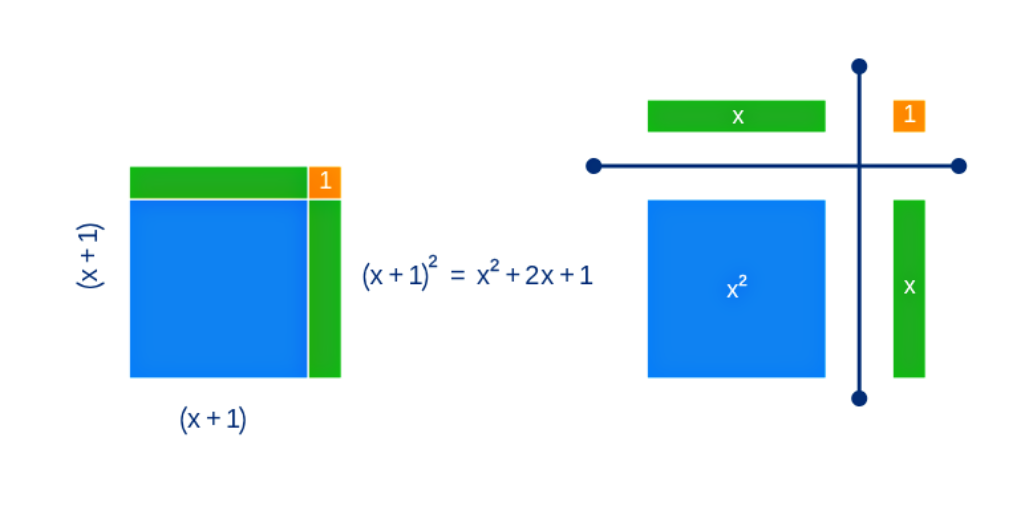
Figura 02: Representação de um quadrado de área (x+3)(x+3)
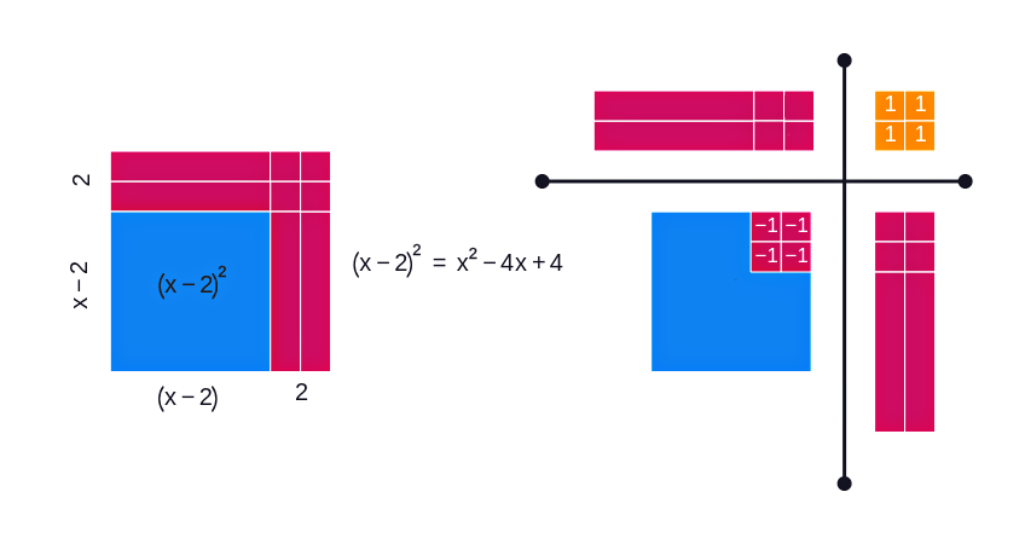
Observe nas Figuras 03 e 04 representações de regiões quadradas dadas por equações do tipo .
Na Figura 03, tem-se uma representação de uma região de equação . Note que:
1 - O quadrado completo, tem lado igual a , logo tem região de equação ;
2 - Deste quadrado, é subtraída a região rosa, ou seja, dois retângulos, onde cada um tem área de altura igual a e largura igual a , ou seja um retângulo de área , como são dois retângulos, retira-se uma área igual a . Observe na decomposição da figura e respectiva operação, que neste processo de retirada de dois retângulos iguais, o pequeno quadrado da região superior é retirado duas vezes;
3 - Por esta razão, observa-se que no desenvolvimento da equação o quadrado unitário é adicionado, pois é a pequena região quadrada que falta para que a área do quadrado azul esteja correta.
2 - Buscamos o quadrado da diferença, ou seja, a região azul, cujo lado tem é dado por , e a região é dada por
De modo análogo a região azul da Figura 04 tem equação
Figura 03: Região quadrada de área (x-1)(x-1)
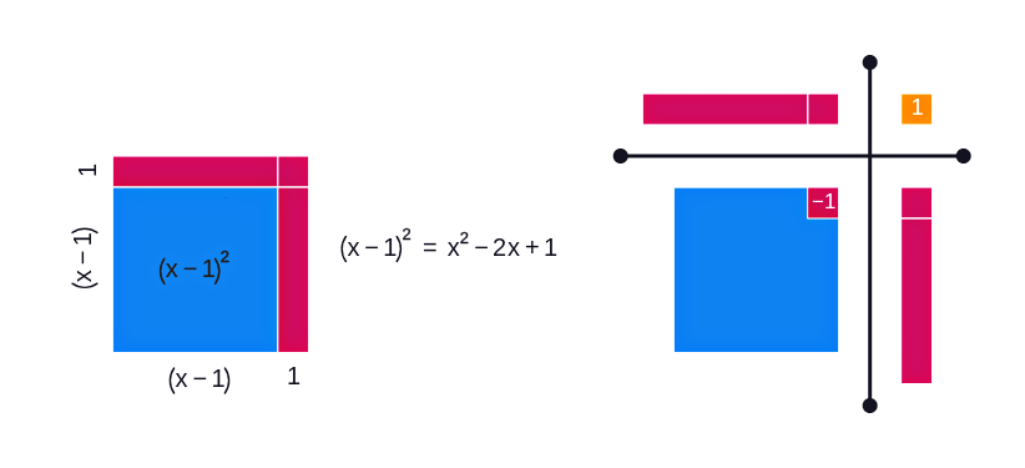
Figura 04: Região quadrada de área (x-2)(x-2)
O método de completar quadrado pode ser utilizado para resolver (encontrar as raízes) equações do segundo grau, no contexto deste estudo, a finalidade da aplicação do método é encontrar uma equação equivalente à uma equação dada.
Neste contexto, o método consiste em completar um trinômio quadrado perfeito e escrevê-lo na forma de um binômio ao quadrado, ou seja,
ou
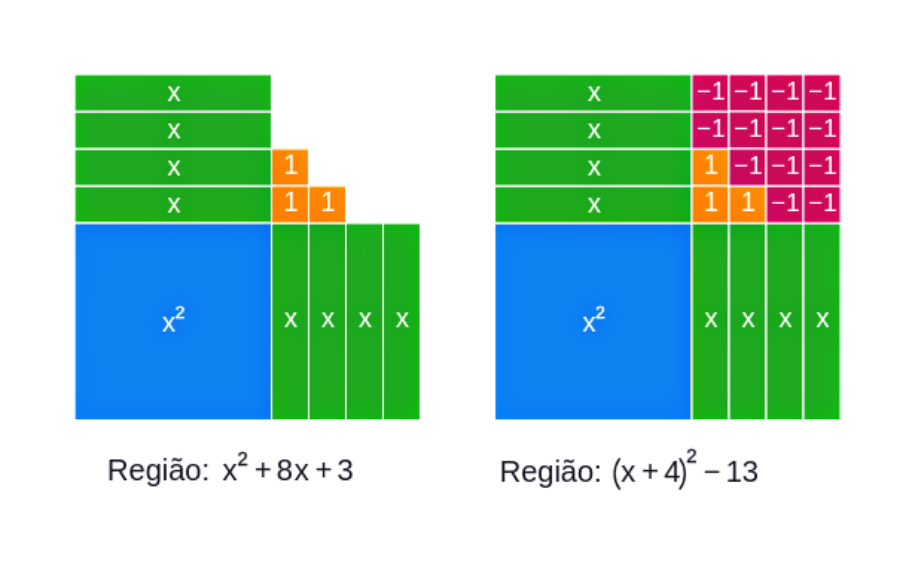
Exemplo 01, representada na Figura 05.
Dada a equação , aplique o método de completar quadrados e reescreva a equação obtendo uma equação na forma fatorada
1 - Inicialmente, tomando a equação dada associe os temos que contém a incógnita
2 - Observe os termos associados e compare com a forma onde e e formam o trinômio , deste modo, o valor que completa o trinômio é o número . Vale ressaltar, que para não alterar a equação, deve-se acrescentar o valor da seguinte forma
.
Portanto , cuja representação geométrica pode ser visualizada na Figura 05.
Outra forma de aplicar o método é tomar a equação dada com , assim
Sabendo que o valor que completa o trinômio quadrado perfeito é , e considerando as propriedades da igualdade, tem-se que
Como tomamos
Figura 05: Representação do método de completar quadrados
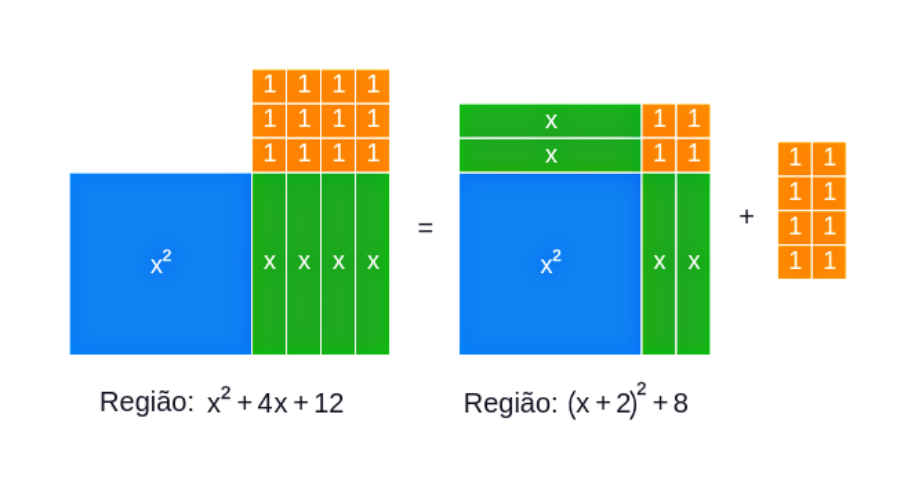
Exemplo 02, representado na Figura 06
Dada a equação , aplique o método de completar quadrados e obtenha uma equação equivalente na forma fatorada.
1 - Tomando a equação dada, associe os termos que contém a incógnita
2- Observe os termos associados e compare com a forma onde e e formam o trinômio , deste modo o valor que completa o trinômio é , então
.
Portanto cuja representação gráfica pode ser observado na Figura 06
Pela segunda forma de aplicar o método (tomando R=0)
Portanto
Figura 06: Representação do método de completar quadrados
Exemplo 03
Dada a equação geral da parábola escreva a equação reduzida e determine os elementos da parábola e faça um esboço do gráfico.
Solução:
Visto que o termo com expoente dois esta na incógnita , a parábola é vertical, portanto a equação que devemos escrever tem a forma com . Tomando a equação dada e aplicando o método de completar quadrados, tem-se que
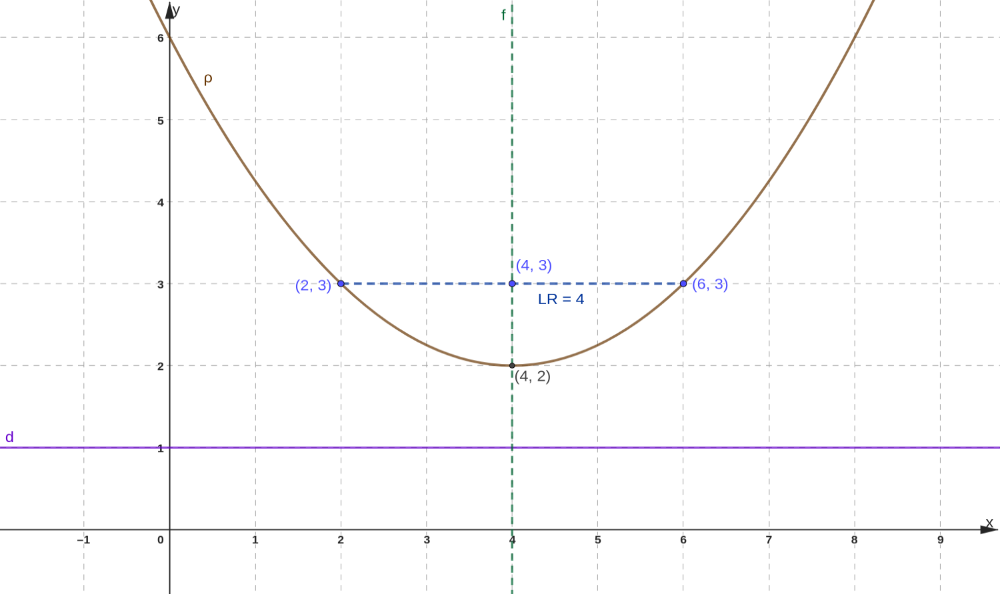
Portanto a equação da parábola na forma reduzida é , de onde obtém-se os seguintes elementos:
1 - Parâmetro: se , então ;
2 - Vértice: ;
3 - Foco: ;
4 - Diretriz: (reta horizontal);
5 - Eixo Focal: (reta vertical);
6 - Latus rectum: .
A Figura 07 é o esboço do gráfico da parábola.
Figura 07: Esboço do gráfico da parábola do exemplo 03
Exemplo 04
Dada a equação geral da parábola escreva a equação reduzida, determine os elementos e faça um esboço da parábola.
Solução:
Visto que o termo quadrático esta na incógnita , a parábola é vertical, de modo que a equação que devemos escrever tem a forma com . Tomando a equação dada e aplicando o método de completar quadrado, tem-se que
Portanto a equação da parábola na forma reduzida é , de onde obtém-se os seguintes elementos:
1 - Parâmetro: ;
2 - Vértice: ;
3 - Foco: ;
4 - Diretriz: ;
5 - Eixo Focal: ;
6 - Lactus rectum: .
A Figura 08 é um esboço do gráfico da parábola.
Figura 08: Esboço do gráfico da parábolda do exemplo 04
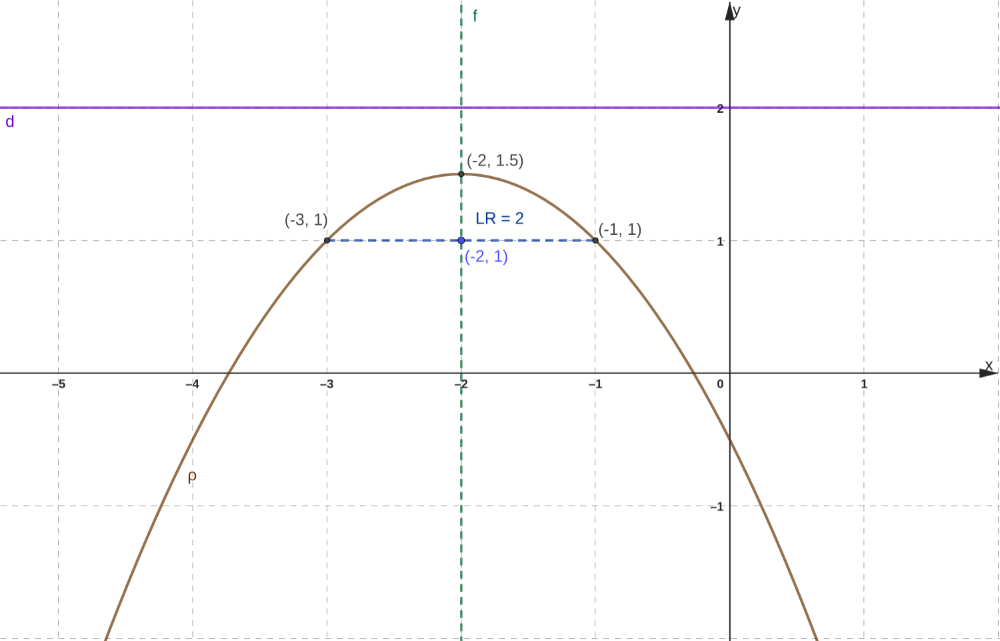
Exemplo 05
Dada a equação geral da parábola escreva a equação reduzida e determine os elementos da parábola e faça um esboço do gráfico.
Solução:
Visto que o termo com expoente dois esta na incógnita , a parábola é horizontal, portanto a equação que devemos escrever tem a forma com . Tomando a equação dada e aplicando o método de completar quadrados, tem-se que
Portanto a equação da parábola na forma reduzida é , de onde obtém-se os seguintes elementos:
1 - Parâmetro: se , então ;
2 - Vértice: ;
3 - Foco: ;
4 - Diretriz: (reta vertical);
5 - Eixo Focal: (reta horizontal);
6 - Latus rectum: .
A Figura 09 é o esboço do gráfico da parábola.
Figura 09: Esboço da parábola do exemplo 05
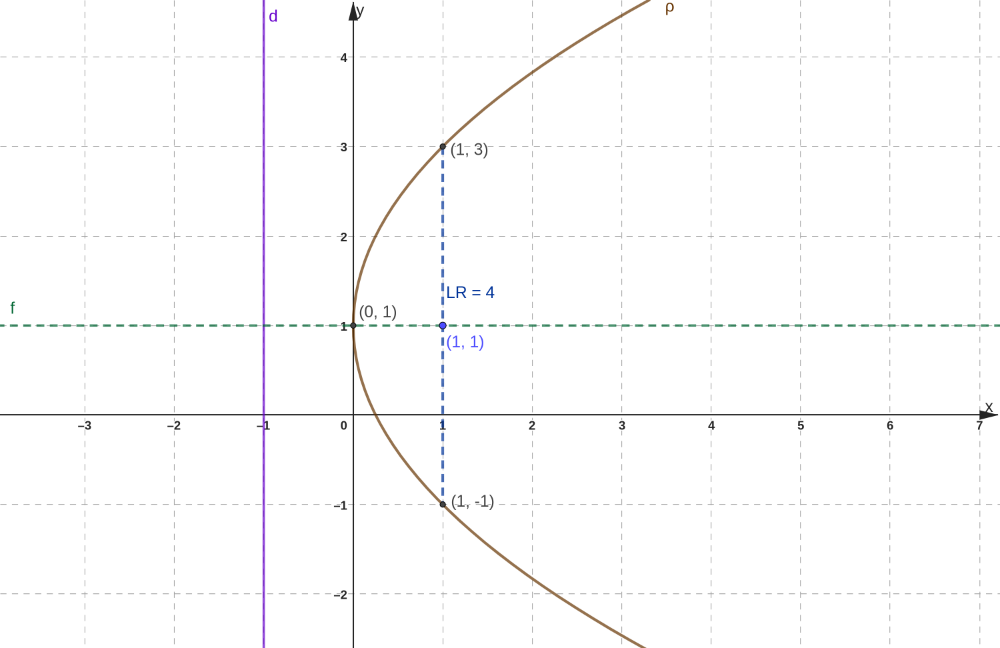
Exemplo 06
Dada a equação geral da parábola escreva a equação reduzida e determine os elementos da parábola e faça um esboço do gráfico.
Solução:
Visto que o termo com expoente dois esta na incógnita , a parábola é horizontal, portanto a equação que devemos escrever tem a forma com . Tomando a equação dada e aplicando o método de completar quadrados, tem-se que
Portanto a equação da parábola na forma reduzida é , de onde obtém-se os seguintes elementos:
1 - Parâmetro: se , então ( a parábola tem abertura voltada a esquerda)
2 - Vértice: ;
3 - Foco: ;
4 - Diretriz: (reta vertical);
5 - Eixo Focal: (reta horizontal);
6 - Latus rectum: .
A Figura 10 é o esboço do gráfico da parábola.
Figura 10: Esboço do grafico da parábolda do exemplo 06
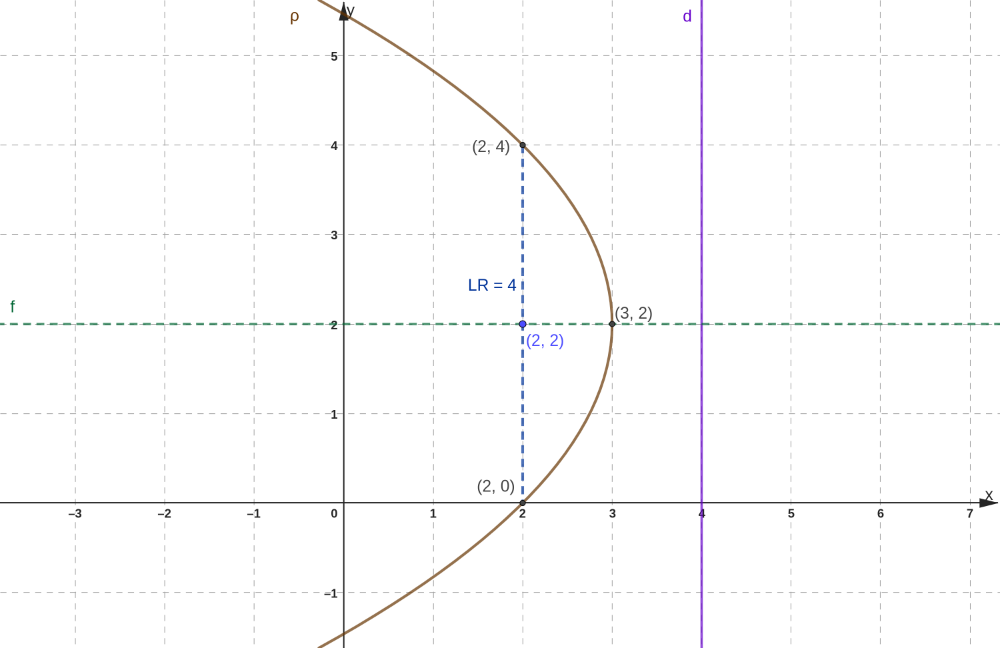
Exemplo 07
Dada a equação geral da parábola escreva a equação reduzida e determine os elementos da parábola e faça um esboço do gráfico.
Solução:
Visto que o termo com expoente dois está na incógnita , a parábola é vertical, portanto a equação que devemos escrever tem a forma com . Tomando a equação dada e aplicando o método de completar quadrados, tem-se que
Portanto a equação da parábola na forma reduzida é , de onde obtém-se os seguintes elementos:
1 - Parâmetro: se , então ;
2 - Vértice: ;
3 - Foco: ;
4 - Diretriz: (reta horizontal);
5 - Eixo Focal: (reta vertical);
6 - Latus rectum: .
A Figura 11 é o esboço do gráfico da parábola.
Figura 11: Esboço do gráfico da parábola do exemplo 11