Box-plot spiegazione
I diagrammi boxplot (scatola-e-baffi), sono stati presentati in modo organico per la prima volta da John W. Tukey nel suo testo del 1977. Sono un metodo grafico diffuso recentemente e reso di uso corrente dai programmi informatici, che possono costruirlo con rapidità.
Servono per rappresentare visivamente quattro caratteristiche fondamentali di una distribuzione statistica di dati campionari:
- la misura di tendenza centrale, attraverso la mediana;
- il grado di dispersione o variabilità dei dati, rispetto alla mediana;
- la forma della distribuzione dei dati, in particolare la simmetria
- sia la semplice presenza che l'individuazione specifica di ogni valore anomalo.
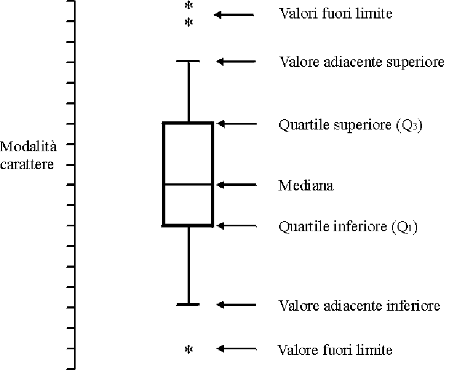
La sua realizzazione richiede una serie di passaggi:
- Ha origine da una linea orizzontale, interna alla scatola, che rappresenta la mediana.
- La scatola (box) è delimitata da due linee orizzontali:
- La distanza tra il terzo (Q3) e il primo quartile (Q1), detta distanza interquartilica, è una misura della dispersione della distribuzione. E’ utile soprattutto quando sono presenti valori anomali, poiché tra il primo e il terzo quartile tra il primo e il terzo quartile (Q3 - Q1) per costruzione sono compresi il 50% delle osservazioni collocate intorno al valore centrale. Un intervallo interquartilico piccolo indica che la metà delle osservazioni ha valori molto vicini alla mediana. L’intervallo aumenta al crescere della dispersione (varianza) dei dati. Inoltre, esso fornisce informazioni anche sulla forma della distribuzione (soprattutto sulla simmetria):
- Le linee che si allungano dai bordi della scatola e che si concludono con altre due linee orizzontali, i baffi (valori adiacenti), delimitano gli intervalli nei quali sono collocati
- Indicando con r la differenza interquartilica r = Q3-Q1 si definiscono le quantità che individuano il Valore Adiacente Inferiore, definito come il valore osservato più piccolo che sia maggiore o uguale a Q1-1,5r: il Valore Adiacente Superiore, definito come il valore osservato più grande che risulta minore o uguale a Q3 + 1,5r: La quantità 1,5 delle due formule è stato proposto da Tukey, ma non ha particolari proprietà. Alla domanda del perché avesse indicato 1,5 e non un altro valore, la risposta di Tukey è stata che la sua scelta era fondata sulla sua esperienza, sul suo “buon senso” statistico.
- Se i due valori estremi - sono contenuti entro l’intervallo [Q1-1,5r ; Q3+1,5r], i due baffi rappresentano i valori estremi e nei dati raccolti non sono presenti valori anomali. - non sono contenuti nell'intervallo, sono definiti valori anomali. Nella rappresentazione grafica del box-plot, i valori anomali, sono segnalati individualmente, poiché costituiscono una anomalia importante rispetto agli altri dati della distribuzione.