Oberfläche der Kugel
Herleitung: Formel für Inhalt der Kugeloberfläche
Die Formel für den Oberflächeninhalt einer Kugel finden wir durch eine "Näherung" (oder "Grenzwertbetrachtung").
Näherung bedeutet: je feiner man die Unterteilung (siehe Bild) wählt, desto näher kommt man der wirklichen Oberfläche.
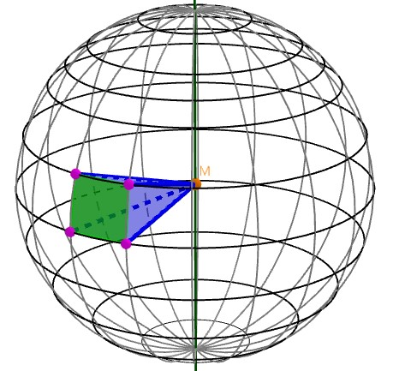
- Wir unterteilen die Oberfläche und erhalten viele Schnittpunkte.
- Wir verbinden die Schnittpunkte mit dem Mittelpunkt M der Kugel und erhalten viele Pyramiden.
- (Denke dir alle Teilflächen mit M verbunden - es entstehen viele Pyramiden)
- Die Grundflächen der Pyramiden sind Trapeze (oder Dreiecke).
- Alle Grundflächen A1 bis An zusammen, ergeben näherungsweise die Oberfläche der Kugel.
- Die Pyramidenhöhen h sind näherungsweise gleich dem Kugelradius r!
- (Je feiner die Unterteilung, desto besser die Näherung!)
- Die Summe aller Pyramidenvolumen:
- A1 bis An ausklammern:
- Die Summe aller Pyramidenvolumen ist näherungsweise gleich dem Kugelvolumen VKugel.
- Die Summe aller Grundflächen A1 bis An ist näherungsweise gleich dem Oberflächeninhalt OKugel.
- Die Pyramidenhöhen h sind näherungsweise gleich dem Kugelradius r.
- also:
- das Kugelvolumen kennen wir bereits:
- also:
- "r und 3 kürzen":