Krug i kružnica

OSNOVNI POJMOVI

KRUŽNICA - skup svih točaka u ravnini jednako udaljenih od zadane točke (središta).

KRUG - skup svih točaka u ravnini čija je udaljenost od određene točke, koju zovemo središte kruga, manja ili jednaka polumjeru kruga. Krug je omeđen kružnicom. POLUMJER (RADIJUS) - dužina koja spaja središte kružnice (kruga ili kugle) s točkom na periferiji. Uobičajena oznaka je r. PROMJER (DIJAMETAR) - pojam koji označava duljinu dužine koja prolazi kroz središte kružnice i čiji krajevi se nalaze na kružnici. Uobičajena oznaka je d. (d=2r) TETIVA - dužina koja spaja dvije točke kružnice. Promjer je tetiva koja prolazi kroz središte kružnice, odnosno najduža tetiva. KRUŽNI LUK - dio kružnice omeđen s neke dvije točke kružnice. KRUŽNI ODSJEČAK - dio kruga omeđen tetivom i pripadajućim kružnim lukom. KRUŽNI ISJEČAK - dio kruga omeđen s dva polumjera i pripadajućim kružnim lukom. POLUKRUŽNICA - dio kružnice omeđen krajnjim točkama promjera kružnice. POLUKRUG - dio kruga omeđen promjerom kruga i pripadajućom polukružnicom.

MEĐUSOBNI POLOŽAJ PRAVCA I KRUŽNICE

Pravac i kružnica mogu zauzimati tri različita položaja u ravnini: 1. Prvac i kružnica nemaju niti jednu zajedničku točku (ne sijeku se) 2. Pravac i kružnica imaju dvije zajedničke točke (sijeku se u dvije točke koje nazivamo SJECIŠTA) Pravac koji siječe kružnicu u dvije točke nazivamo SEKANTA. 3.Pravac i kružnica imaju jednu zajedničku točku (dodiruju se u jednoj točki koju nazivamo DIRALIŠTE) Pravac koji dodiruje kružnicu u jendoj točki nazivamo TANGENTA.

MEĐUSOBNI POLOŽAJ DVIJU KRUŽNICA

Dvije kružnice mogu zauzimati tri različita položaja u ravnini: 1. Kružnice nemaju niti jednu zajedničku točku (ne sijeku se) 2. Kružnice imaju dvije zajedničke točke (sijeku se u dvije točke koje nazivamo SJECIŠTA) 3. Kružnice imaju jednu zajedničku točku dodiruju se u jednoj točki koju nazivamo DIRALIŠTE)

POUČAK O SREDIŠNJEM I OBODNOM KUTU

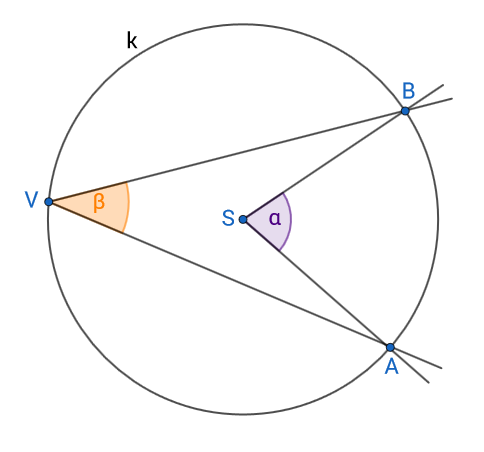
Središnji kut- kut kojemu je vrh u središtu kružnice. Središnji kut luka AB kružnice k – kut čiji je vrh u središtu kružnice i čiji krakovi sijeku kružnicu u točkama A i B Obodni kut - kut kojem je vrh na kružnici a čiji krakovi sijeku tu kružnicu. Obodni kut luka AB kružnice k – kut čiji je vrh na kružnici i čiji krakovi sijeku kružnicu u točkama A i B Svakom obodnom kutu pripada točno jedan središnji kut (nad istim kružnim lukom). Središnji je kut dvostruko veći od pripadnog obodnog kuta a =2b.

POUČAK O OBODNIM KUTOVIMA NAD ISTIM KRUŽNIM LUKOM

Svi obodni kutovi nad istim kružnim lukom jednakih su veličina, a ima ih beskonačno mnogo.

TALESOV POUČAK

Svaki obodni kut nad promjerom kružnice je pravi kut.

OPSEG I POVRŠINA KRUGA

Opseg kruga je duljina kružnice koja omeđuje zadani krug. Opseg kruga izračunava se formulom O=2rπ, gdje je r radijus (polumjer) kruga, a π (pi) beskonačan broj koji iznosi 3.1415... Površina kruga izračunava se formulom P=r^2π

DULJINA KRUŽNOG LUKA

Kružni luk (l) dio je kružnice omeđen dvjema točkama. Njegova duljina izračunava se formulom l=2rπ(a/360), gdje je α središnji kut zadanog luka u stupnjevima i r radijus kružnice.

POVRŠINA KRUŽNOG ISJEČKA

Dio kruga omeđen s dva polumjera r i pripadajućim kružnim lukom l zove se kružni isječak. Njegovu površinu računamo po formuli P=r^2π(a/360)

JEDNADŽBA KRUŽNICE

Jednadžba kružnice sa središtem u točki S (p, q) i polumjerom r jest (x-p)² + (y-q)² = r² Jednadžba kružnice sa središtem u ishodištu koordinatnog sustava i polumjerom r jest x² + y² = r²