3. Herramientas teóricas que componen el enfoque ontosemiótico
El Enfoque Ontosemiótico (EOS) es un marco teórico que ha surgido en el seno de la Didáctica de las Matemáticas, con el propósito de articular diferentes puntos de vista y nociones teóricas sobre el conocimiento matemático, su enseñanza y aprendizaje.
El punto de partida del EOS es la formulación de una ontología de objetos matemáticos que tiene en
cuenta el triple aspecto de la matemática como actividad de resolución de problemas, socialmente
compartida, como lenguaje simbólico y sistema conceptual.
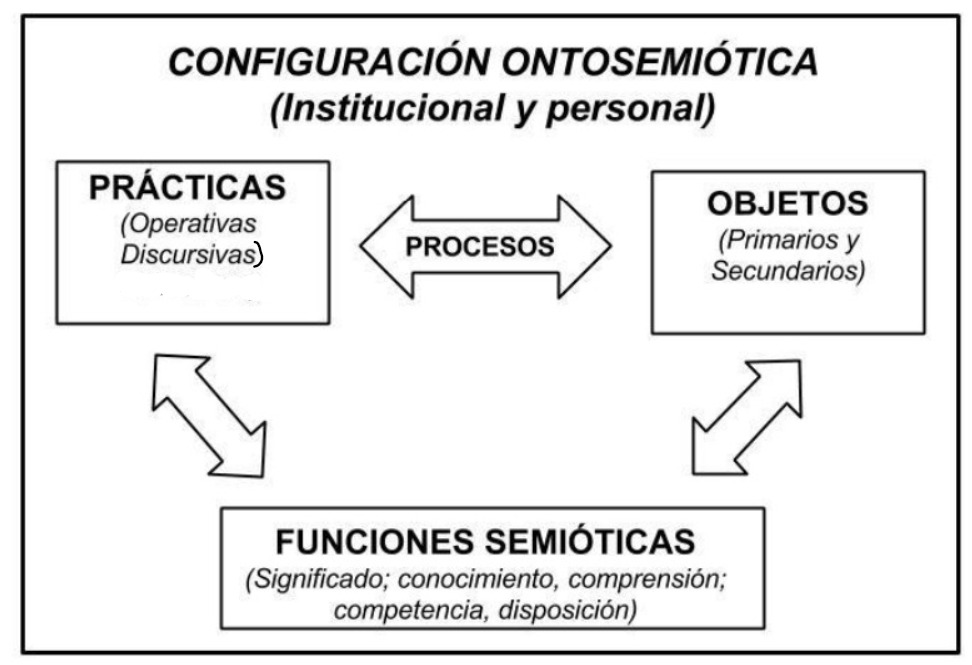
3.1 Sistemas de prácticas operativas y discursivas ligadas a tipos de problemas
Se considera práctica matemática a toda actuación o expresión (verbal, gráfica, etc.) realizada por
alguien para resolver problemas matemáticos, comunicar a otros la solución obtenida, validarla o
generalizarla a otros contextos y problemas (Godino y Batanero, 1994, p. 334).
En el estudio de las matemáticas, más que una práctica particular ante un problema concreto, interesa
considerar los sistemas de prácticas (operativas y discursivas). La relatividad socioepistémica y cognitiva de los significados, entendidos como sistemas de prácticas, y su utilización en el análisis didáctico lleva a introducir la tipología básica de significados (Godino, 2003, p. 141).
• Con relación a los significados institucionales
-Evaluado: el subsistema de prácticas que utiliza el docente para evaluar los aprendizajes.
-Implementado: en un proceso de estudio específico es el sistema de prácticas efectivamente implementadas por el docente.
-Pretendido: sistema de prácticas incluidas en la planificación del proceso de estudio.
-Referencial: sistema de prácticas que se usa como referencia para elaborar el significado pretendido.
• Con relación a los significados personales
-Global: corresponde a la totalidad del sistema de prácticas personales que es capaz de manifestar potencialmente el sujeto relativas a un objeto matemático.
-Declarado: da cuenta de las prácticas efectivamente expresadas a propósito de las pruebas de evaluación propuestas, incluyendo tanto las correctas como las incorrectas desde el punto de vista institucional.
-Logrado: corresponde a las prácticas manifestadas que son conformes con la pauta institucional establecida, teniendo en cuenta los significados iniciales o previos de los estudiantes y los que finalmente alcancen.
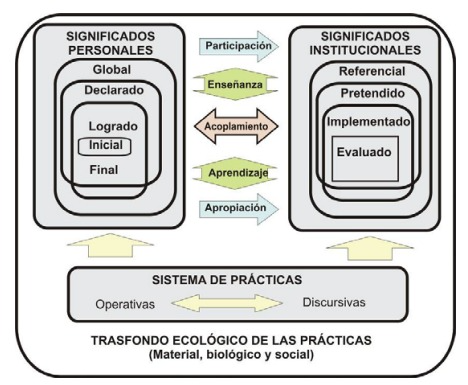
3.2. Emergencia de los objetos matemáticos
En el EOS se considera que los objetos matemáticos son emergentes de sistemas de prácticas. Dicha emergencia es un fenómeno complejo cuya explicación implica considerar, como mínimo, dos niveles de objetos que emergen de la actividad matemática.
-En el primer nivel tenemos aquellas entidades que se pueden observar en un texto matemático (problemas, definiciones, proposiciones, etc.).
-En un segundo nivel tenemos una tipología de objetos que emerge de las distintas maneras de ver, hablar, operar, etc. sobre los objetos del nivel anterior.
3.2.1. Primer nivel.
Configuraciones de objetos intervinientes y emergentes de los sistemas de prácticas
Para la realización de una práctica matemática y para la interpretación de sus resultados como satisfactorios se necesita poner en funcionamiento determinados conocimientos
Cuando un agente realiza y evalúa una práctica matemática activa un conglomerado formado por situaciones – problemas, lenguajes, conceptos, proposiciones, procedimientos y argumentos, articulado en la configuración de (Font y Godino, 2006, p. 69).
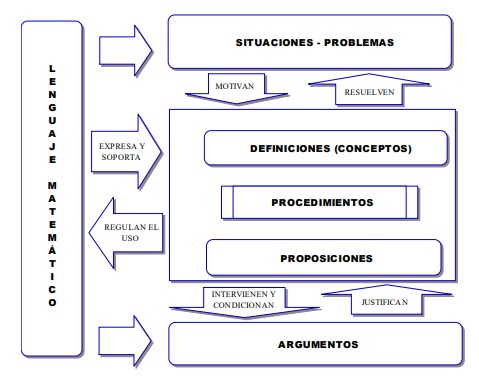
- Elementos lingüísticos: (términos, expresiones, notaciones, gráficos, ...) en sus diversos registros (escrito, oral, gestual, ...)
- Situaciones – problemas: (aplicaciones extra-matemáticas, tareas, ejercicios, ...)
- Conceptos- definición: (introducidos mediante definiciones o descripciones) (recta, punto, número, media, función, ...)
- Proposiciones: (enunciados sobre conceptos, ...)
- Procedimientos: (algoritmos, operaciones, técnicas de cálculo, ...)
- Argumentos: (enunciados usados para validar o explicar las proposiciones y procedimientos, deductivos o de otro tipo, ...).
3.2.2. Segundo nivel. Atributos contextuales
Los objetos matemáticos que intervienen en las prácticas matemáticas y los emergentes de las mismas, según el juego de lenguaje en que participan, pueden ser consideradas desde las siguientes facetas o dimensiones duales (Godino, 2002)
- Personal – institucional:
- Ostensivo – no ostensivo:
- Expresión – contenido:
- Extensivo – intensivo (ejemplar - tipo):
- Unitario – sistémico.
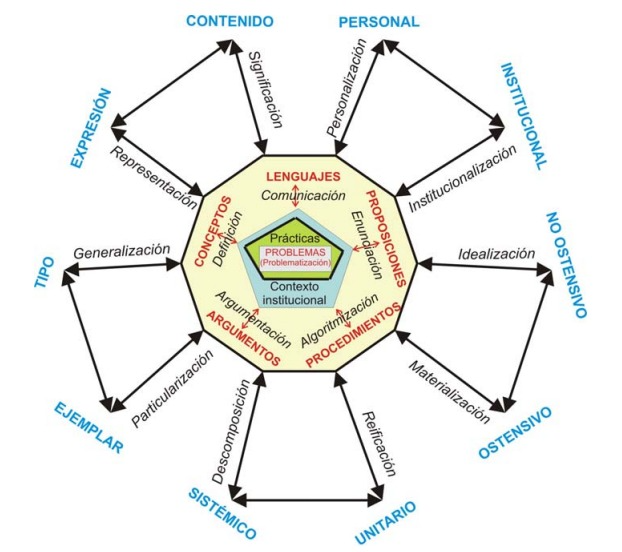
3.2.3 Procesos
En el EOS no se intenta dar, de entrada, una definición de “proceso” ya que hay muchas clases diferentes de procesos; se puede hablar de proceso como secuencia de prácticas, de procesos
cognitivos, metacognitivos, procesos de instrucción, procesos de cambio, procesos sociales, etc
Tanto las dualidades como las configuraciones de objetos primarios se pueden analizar desde la perspectiva proceso-producto.
En cuanto al primer nivel (problemas, definiciones, proposiciones, procedimientos y argumentos) tiene lugar mediante los respectivos procesos matemáticos de comunicación, definición, enunciación, elaboración de procedimientos (algoritmización, rutinización, ...) y argumentación.
Por otra parte, las dualidades dan lugar a los siguientes procesos cognitivos/ epistémicos: institucionalización – personalización; generalización –particularización; análisis/descomposición – síntesis/reificación; materialización/concreción –idealización/ abstracción; expresión/representación – significación.