4 Multiplikation eines Vektors mit einer Zahl
Kleine Schritte Super Mario!
Hier findest du den Hefteintrag zur heutigen Stunde. Übertrage ihn in dein Heft und sieh dir dazu das Erklärvideo an.
Erklärvideo: Hefteintrag
Hefteintrag Multiplikation eines Vektors mit einer Zahl
Jetzt geht es ans Üben :)
BASISAUFABEN
Suche dir aus den Aufgaben jeweils mindestens 2 Teilaufgaben aus, die du rechnen möchtest. Wenn du eine Aufgabe falsch gerechnet hast, dann rechne eine Weitere, bis du dich bei der Bearbeitung sicher fühlst.
Buch S. 101f Nr. 2, 3, 4, 9
Aufgabe 2

Lösungen 2
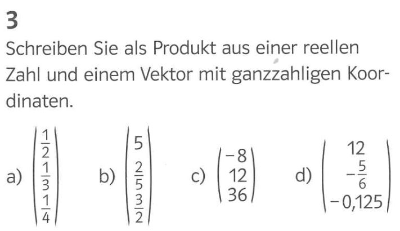
Lösungen 3 (Individuelle Lösungen möglich)
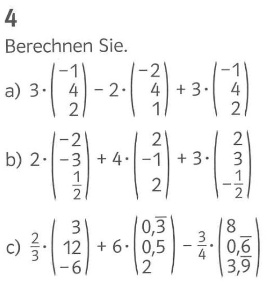
Lösungen 4

Lösungen 9
FORTGESCHRITTENAUFGABEN
Nach den Basisaufgaben seid ihr bereit für "the next level"! Berechne hier wieder jeweils 2 Teilaufgaben. Wenn du Aufgaben falsch gelöst hast oder dir unsicher bist, dann berechne noch weitere Aufgaben. Versuche hier auch Aufgaben mit drei Koordinaten zu lösen!
Buch S. 102f Nr. 6, 11, 14
![[color=#0000ff][b]Hinweis: Diese Aufgaben kann man durch einen "Blick" lösen (z.B. 4 mal 2 ist 8 -> x=4). Vergiss aber nicht, alle anderen Koordinaten zu überprüfen (z.B. 4 mal 1 ist 4 -> passt!). Falls es dort nicht stimmt, gibt es keine Lösung.
[/b][/color][b][color=#ff00ff]Alternativ kannst du die Aufgabe mit einem Gleichungssystem lösen, z.B. 6d:
I. 1 = -2x
II. 2 = -4x
III. 3 = -6x[/color][/b]](https://www.geogebra.org/resource/nxyvbbz8/1nW8nwnxpoGuY787/material-nxyvbbz8.png)
Lösungen 6

Lösungen 11
![[color=#0000ff][b]Hinweis: Löse wie eine normale Gleichung auf, indem du den Vektor x auf einer Seite isolierst. (Vergiss die Regel "Punkt vor Strich" nicht!)[/b][/color]](https://www.geogebra.org/resource/qfdw9gmx/pS5Gyc1kXpTJYTaM/material-qfdw9gmx.png)
Lösungen 14
Der Mittelpunkt einer Strecke
Sieh dir das Applet an. Begründe mit Hilfe von Vektoren, dass man, um den Mittelpunkt einer Strecke zu finden, die im Applet stehende Formel verwenden kann. M ist der Mittelpunkt der Strecke [AB].
Lösung
Hinweis: diesen Zusammenhang findest du auch in der Merkhilfe. Er kommt so oft vor, dass du ihn auswendig wissen solltest.

Lösung 8
Freiwillige Profiaufgaben:
Wer seine Beweiskünste testen möchte, kann noch die folgenden Aufgaben lösen. Wenn ihr mir die Lösung schickt oder auf Mebis hochladet, werde ich diese für euch korrigieren.
Buch S. 101f Nr. 5a, Nr. 13
Freiwillige Basisaufgaben auf Mathegym:
Wer lieber noch einmal Basisaufgaben üben möchte, kann dies über die folgenden Aufgaben bei MatheGym tun.
