Triángulo rectángulo y Teorema de Pitágoras - Lección 01-05
Triángulo rectángulo
Triángulo rectángulo es todo triángulo en el cual uno de sus ángulos es un ángulo recto (mide 90°).
En el applet siguiente se muestra el triángulo rectángulo ABC, rectángulo en A.
Lados del triángulo rectángulo
- Catetos: Son los lados que forman el ángulo recto. Lados b y c.
- Hipotenusa: Es el lado que se opone al ángulo recto. Lado c. Su longitud es mayor que la longitud de cualquiera de los dos catetos.
Ángulos agudos en el triángulo rectángulo
Los ángulos agudos de un triángulo rectángulo son complementarios. La suma de sus medidas es 90°.
Actividades.
1. Ángulos en el triángulo rectángulo.
Utilice el deslizador del applet siguiente para ver la animación de los ángulos agudos del triángulo rectángulo.
Teorema de Pitágoras.
En todo triángulo rectángulo la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa.
2. Animación de demostración geométrica de H Perigal del Teorema de Pitágoras
La animación consta de dos secciones secuenciales: una construcción auxiliar y la animación propiamente dicha.
- Construcción auxiliar. Haga clic en el botón Construcción auxiliar. El segmento ML es paralelo a la hipotenusa y pasa por K que es el centro del cuadrado ABFG.
El segmento ON es mediatriz de ML (perpendicular que pasa por su centro).
La construcción auxiliar se hace sobre el cuadrado del cateto mayor.
- Inicia traslación. Haga clic en este botón para trasladar los 4 polígonos que se forman en el cuadrado ABFG así como el cuadrado ACIH.
** La animación también se puede ejecutar manualmente.
3. Teorema de Pitágoras - comprobación numérica
El applet siguiente muestra que sobre cada lado del triángulo rectángulo ABC se ha dibujado un cuadrado.
Utilice los deslizadores para modificar las medidas de los catetos.
Active la tabla de valores para verificar el cumplimiento del Teorema de Pitágoras.
Así por ejemplo, si cateto1 = 3, cateto2 = 4, entonces hipotenusa = 5 porque :
Con el teorema de Pitágoras se presentan dos casos:
a. Cuando se conoce la medida de los dos catetos y se desconoce la media de la hipotenusa.
Ejemplo:
En un triángulo rectángulo los catetos son m y n y la hipotenusa p.
Si m = 6 u y n = 10 u, calcular la medida de la hipotenusa.
Fórmula del teorema de Pitágoras para este triángulo:
p = 11.66 u
Se reitera que la medida de la hipotenusa siempre es mayor que la medida de cada uno de los catetos.
b. Cuando se conoce la medida de un cateto y de la hipotenusa y se desconoce la media del otro cateto.
Ejemplo:
Los catetos de un triángulo rectángulo son x y y y la hipotenusa es z.
Si x = 8 u y z = 14 u, calcular la medida del otro cateto.
Fórmula del teorema de Pitágoras para este triángulo:
Como el término desconocido es se hace transposición de términos:
y = 11.49 u
Observación: Cuando se necesita calcular la medida de un cateto conociendo la medida de la hipotenusa y del otro cateto, la fórmula del teorema de Pitágoras queda así:
Siempre la medida de un cateto es menor que la medida de la hipotenusa.
Resuelva el siguiente cuestionario:
4. Un triángulo rectángulo es isósceles. Por lo tanto, las medidas de los ángulos agudos son
5. Los lados de un cuadrado miden 8 cm cada uno. La medida de la diagonal del cuadrado mide
6. En un rectángulo la base mide 10 cm y la diagonal 15 cm. La medida de la altura del rectángulo es
7. Una escalera tiene una longitud de 3 m y se apoya en una pared vertical. A qué altura llega el extremo superior de la escalera cuando el extremo inferior está a 80 cm de la pared.
Responda las preguntas 8, 9, 10 y 11 de acuerdo con la figura siguiente. Las medidas están dadas en metros.
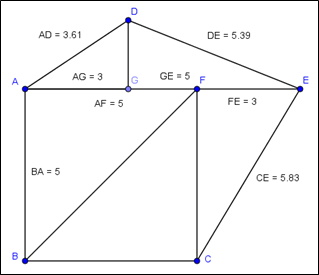
8. Calcule la medida del segmento BF. Justifique su respuesta.
9. Calcule la medida del segmento DG. Justifique su respuesta.
10. Calcule la medida del segmento CF. Justifique su respuesta.
11. Calcule la medida del segmento GD. Justifique su respuesta.