Μέγιστα και ελάχιστα με Ε. Γ
Σταθερό εμβαδόν - Ελάχιστη υποτείνουσα
Στη δραστηριότητα επιχειρούμε να αναδείξουμε τη σημασία των πολλαπλών δυναμικών αναπαραστάσεων για τη σχεσιακή κατανόηση στο μαθηματικό συλλογισμό.
Συγκεκριμένα, από δυναμικές αναπαραστάσεις με γεωμετρικό περιεχόμενο, νοηματοδοτούνται αλγεβρικές σχέσεις και αντίστροφα: από δ.α με συναρτησιακό ή/και αλγεβρικό περιεχόμενο, νοηματοδοτούνται γεωμετρικές μεταβολές.
Πρόβλημα (γεωμετρική διατύπωση)
Από όλα τα ορθογώνια τρίγωνα ΑΒΓ με σταθερό εμβαδόν, να βρεθεί εκείνο που έχει την ελάχιστη υποτείνουσα ή από όλα τα ορθογώνια με σταθερό εμβαδόν, ποιο έχει ελάχιστη διαγώνιο;
Αλγεβρική Αναδιατύπωση του προβλήματος
Από όλους τους θετικούς πραγματικούς αριθμούς x,y με σταθερό γινόμενο, ποιοι έχουν ελάχιστο άθροισμα τετραγώνων;
Οδηγίες
Στο δόμημα εμφανίζεται ένα ορθογώνιο τρίγωνο ΑΒΓ με σταθερό εμβαδόν Ε, το οποίο ρυθμίζεται από το δρομέα Ε. Στο δεξί παράθυρο, εμφανίζεται η γραμμή που διαγράφει ένα σημείο Ρ που έχει συντεταγμένες (γ,α) με γ,α την κάθετη πλευρά και την υποτείνουσα αντίστοιχα του τριγώνου ΑΒΓ.
Πειραματισμός - Εικασία
- Σύρετε το σημείο Β σε διάφορες θέσεις. Μπορείτε από το γράφημα του σημείου Ρ να εικάσετε πότε η υποτείνουσα α γίνεται ελάχιστη;
- Eπαναλάβατε τον πειραματισμό και για άλλες τιμές του εμβαδού Ε. Πατήστε το κουμπί "min" για να ελέγξετε την εικασία σας.
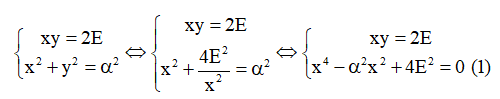
H εξίσωση (1) αν θέσουμε x2=ω, γράφεται ισοδύναμα: ω2-α2ω+4Ε2=0. (2)
Πατήστε το διακόπτη "1η αναπαράσταση". Εμφανίζεται η γραφική παράσταση p (παραβολή) του τριωνύμου
- Πειραματιστείτε με διάφορες θέσεις του σημείου Β.
- Τί φαίνεται να ισχύει για τις σχετικές θέσεις της παραβολής p με τον άξονα xx΄;
- Εκφράστε αλγεβρικά τις παρατηρήσεις σας από το προηγούμενο ερώτημα.
- Μπορείτε να χρησιμοποιήσετε την προηγούμενη σχέση για την απόδειξη της εικασίας;
Απόδειξη1

2η απόδειξη (αλγεβρική)
Ισχύει ότι:
H τελευταία σχέση προδιαθέτει για το σχηματισμό ...(;)
Απόδειξη2
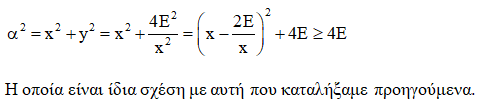
3η απόδειξη (Γεωμετρική)
Ανοίξτε το διακόπτη "3η αναπαράσταση". Εμφανίζονται το ημικύκλιο διαμέτρου ΑΒ και η διάμεσος ΛΜ.
- Ποια σχέση υπάρχει μεταξύ των υψών ΑΝ και ΛΜ;
- Χρησιμοποιώντας τον τύπο εμβαδού του τριγώνου, μπορείτε να αποδείξετε τον ισχυρισμό;
Απόδειξη
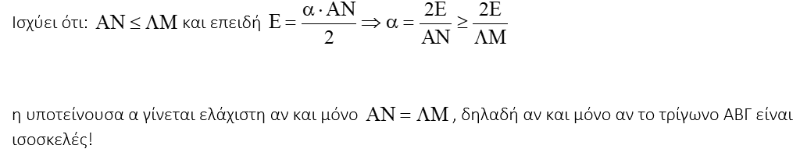
2η Αναπαράσταση (αναλυτική γεωμετρία)
Ανοίξτε το διακόπτη "2η αναπαράσταση".Εμφανίζονται οι γραφικές παραστάσεις του κύκλου και της υπερβολής καθώς και οι εφαπτομένες της υπερβολής στα σημεία της Η και Θ.
- Σύρετε το σημείο Β σε διάφορες θέσεις.
- Τί παρατηρείτε για τις σχετικές θέσεις των δύο κωνικών τομών;
- Τί φαίνεται να ισχύει με τη σχετική θέση τους, όταν η υποτείνουσα α γίνει ελάχιστη;
- Μπορείτε να εικάσετε από το προηγούμενο ερώτημα, πότε δύο κωνικές τομές θα λέμε ότι εφάπτονται σε κάποιο κοινό τους σημείο;