Construcciones geométricas de polígonos regulares
Contenido
Esta actividad es una compilación de construcción de polígonos regulares por varios métodos.
- Construcción de polígonos regulares cuando se da el lado del polígono
- Construcción de polígonos regulares cuando se da el radio de la circunferencia circunscrita
- Construcción especial del hexágono regular y del triángulo regular (equilátero)
Polígono regular es todo polígono que tiene sus lados y sus ángulos internos congruentes.
Un polígono regular se puede construir a partir del lado del polígono y también a partir del radio de la circunferencia circunscrita.
A continuación se muestran dos formas de construir cuando se da el lado y dos formas cuando se da la circunferencia circunscrita.
Construcción de polígonos regulares dado el lado del polígono:
El lado del polígono es el segmento AB.
Construcción No. 1:
1. Construcciones inciales
- Por los extremos del lado, trazar circunferencias con radio AB. Las dos circunferencias se intersecan en los punto Q6 y E.
- Trazar la recta que pasa por estos dos puntos.
- Trazar circunferencia con centro Q6 con radio Q6A. Se determina el punto F.
El objetivo es dividir la distancia FQ6 en seis partes iguales, aplicando el teorema de Thales.
2. Semirrecta de construcción FG
- Trazar semirrecta FG. El punto G es libre, se puede ubicar en cualquier parte.
- Dividir le semirrecta FG en tantas partes como lados tenga el polígono. En este caso, hasta 13 lados.
La longitud de cada división es libre. En el applet se determina con el deslizador dFP1.
3. Semirrecta Q6P6
4. Paralelas a Q6P6
- Trazar paralelas a Q6P6 por los puntos P5 hasta P13.
5. Centro de los polígonos
Son los puntos de intersección de cada paralela con la recta FQ6 y determinan el centro de la circunferencia que pasa por A y por B de acuerdo con el número de lados del polígono.
6. Construcción del polígono
- Seleccionar el número de lados del polígono. Se hace con el deslizador n. Por ejemplo, n = 8 (octágono)- Trazar circunferencia con centro en Q8 y radio Q8A. Se obtiene la circunferencia circunscrita al polígono
- Dividir con el compás la circunferencia circunscrita. Se trazan sucesivamente circunferencias con centro en los extremos del lado y radio el mismo lado. Se obtienen los vértices del polígono.
Observación: Este es un método aproximado.
Construcción No. 2:
- Calcular la medida del ángulo interno de polígono.
Si n = 10, Se recuerda la fórmula:
- Medir con el transportador y por un extremo del lado, el ángulo calculado. La longitud del lado BC se puede determinar con una circunferencia con centro en B y radio BA.
- Repetir el proceso para los demás lados.
Se puede observar que si el lado del polígono regular se mantiene constante, el radio de la circunferencia circunscrita (segmento VA) es mayor a medida que el número de lados se hace mayor.
Construcción de polígonos regulares dado el radio de la circunferencia circunscrita
Construcción No. 1
La circunferencia circunscrita tiene centro en H y su radio es R
1. Construcciones iniciales
- Trazar una circunferencia con centro en H y radio igual a R
- Trazar un diámetro por un punto de la circunferencia (punto D)
- Trazar una circunferencia con centro en cada extremo del diámetro. Se intersecan en el punto A
2. Semirrecta de construcción DG y Puntos Qn
Trazar semirrecta DG y dividirla en partes iguales. El punto G es libre. El tamaño de cada división se define con el deslizador dDD1. Se obtienen los puntos Dn
3. Defina el número de lados
Utilizar el deslizador n para mostrar la construcción de cada polígono. Se muestra desde 5 hasta 10 lados:
- Trazar semirrecta Dn y que pasa por F. Si n = 5 la semirrecta va de D5 y pasa por F
- Trazar semirrecta paralela a D5F que pase por D2. Se interseca con el diámetro en el punto Qn
- Trazar recta que pasa por A y por Qn. Esta recta interseca a la circunferencia original en B5 porque n = 5. El segmento DB5 es el lado del polígono.
- Trazar circunferencias sucesivas con radio igual al lado para obtener los otros vértices.
Observación: Este también es un método aproximado.
Construcción No. 2:
- Calcular la medida del ángulo central del polígono.
Si n = 5, Se recuerda la fórmula,
- Dividir la circunferencia en n partes utilizando el transportador. El segmento AB es el lado del plígono.
Se puede observar que si el radio de la circunferencia circunscrita se mantiene constante, el lado del polígono es menor a medida que el número de lados se hace mayor.
Procedimiento especial para construir un hexágono y un triángulo regulares inscritos
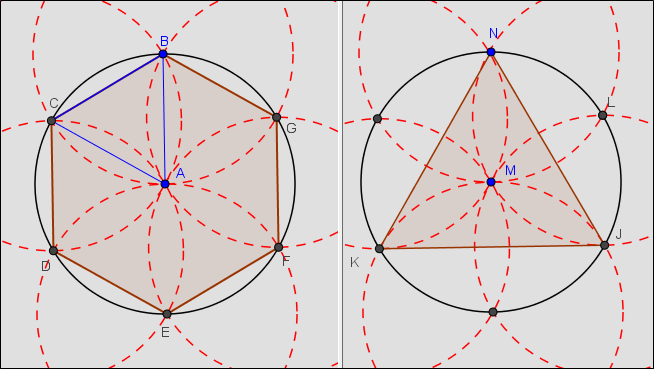
Construcción del hexágono BCDEFGB
- Trazar una circunferencia con centro A y radio AB
- Con centro en B y con el mismo radio, trazar otra circunferencia. Se intersecan en C y G.
- Trazar circunferencia con el mismo radio con centro en C y en G. Se obtenen los vértices D y F
- Repetir el proceso con circunferencias en D y F. Las dos coinciden en el vértice E
Justificación:
El triangulo central ABC es un triángulo equilátero porque:
- el ángulo central en un hexágono mide 60°
- la suma de las medidas de los ángulos ABC y ACB del triángulo ABC, equivale a 180° - 60° = 120°
- el triángulo ABC es isósceles porque los lados AB y AC son congruentes e iguales al radio
- los ángulos ABC y ACB son congruentes porque el triángulo ABC es isóscles. Por lo tanto los dos ángulos son congruentes e iguales a 60°.
- los lados AB, BC y CA son congruentes e iguales al radio
Como conclusión, la medida del lado de un hexágono regular es igual a la medida del radio de la circunferencia circunscrita.
Construcción del triángulo NKJN
Hacer el proceso de construcción del hexágono y seleccionar sólo tres vértices no consecutivos.