Kongruenz und Kongruenzsätze (Dokumentation)
Kongruenz im Bildungsplan
Zunächst soll es um die Inhalte, die explizit im Bildungsplan stehen, gehen. Die Schülerinnen und Schüler sollen in der Unterrichtseinheit zum Thema "Kongruenz und Kongruenzsätze" lernen, Figuren auf Kongruenz zu überprüfen und einzelne Kongruenzsätze in ersten geometrischen Beweisen anwenden können. Zentraler Aspekt der Lerneinheit ist also auch eine Einführung in formale Beweise und in allgemeine Beweisstrukturen. Deshalb ist das Thema "Kongruenz und Kongruenzsätze" im Bildungsplan in Baden-Württemberg auch erst in den Klassenstufen 9/10 verankert, da die Schülerinnen und Schüler in diesem Alter in der Lage sind, formale Beweise nachzuvollziehen und diese gegebenenfalls auch selber durchführen können. Als Voraussetzung zu dieser Unterrichtssequenz lernen die Schülerinnen und Schüler in den Klassenstufen zuvor grundlegende Eigenschaften geometrischer Objekte kennen, Üben sich im Umgang mit Geodreieck und Lineal und lernen, Dreiecke zu konstruieren und Konstruktionsbeschreibungen zu erarbeiten. Zudem werden in den Klassenstufen 7 und 8 auch schon einige geometrische Sätze, wie zum Beispiel der Nebenwinkelsatz, der "Satz des Thales" oder der Satz des gleichschenkligen Dreiecks eingeführt, sodass die Schülerinnen und Schüler bereits mit mathematischen Sätzen vertraut sind. Definitonen von Kongruenz Es gibt zwei Definitonen für den Begriff Kongruenz:
- Zwei Figuren heißen kongruent zueinander oder deckungsgleich, wenn man eine der Figuren so bewegen kann, dass sie mit der anderen zur Deckung kommt. (nach Cukrowicz und Zimmermann 2000, MatheNetz 7N, S.107)
- Zwei Figuren A und B sind kongruent (deckungsgleich) zueinander, wenn sie in der Form und in den Maßen übereinstimmen. Zueinander kongruente Figuren passen genau aufeinander. (Griesel u. a. 2004, Mathematik heute 3 – Baden-Württemberg, S.76)
Um im Sinn der ersten Definition zu überprüfen, ob zwei Figuren kongruent sind, können die Figuren so gespiegelt, gedreht oder verschoben werden, dass sie deckungsgleich aufeinander liegen. Das Überprüfen der Kongruenz ist also ein dynamischer Prozess und kann gut durch haptisches Arbeiten durchgeführt werden. Zum Beispiel können die Schülerinnen und Schüler mit ausgeschnittenen Pappdreiecken an diese Definiton der Kongruenz herangeführt werden und intuitiv prüfen, ob die Dreiecke so bewegt werden können, ob sie deckungsgleich sind. Laut der zweiten Definition sind zwei Figuren kongruent, wenn alle entsprechenden Seiten gleich lang sind und alle entsprechenden Winkel gleich weit sind. Um zu überprüfen, ob zwei Figuren kongruent sind, können also alle Seitenlängen und Winkelweiten gemessen werden. Aufgabenstellung zu Definition 2: Überprüfe, ob die Dreiecke A und B in Abb. 1 kongruent zueinander sind. Miss dazu zuerst alle Winkel und Seiten der Dreiecke. Vergleiche dann, ob alle entsprechenden Winkel gleich groß und alle entsprechenden Seiten gleich lang sind.
Abb. 1
- sss
- sws
- wsw
- Ssw
Abb. 2
- Als Beweismittel dienen vor allem die Kongruenzsätze für Dreiecke und wenige weitere Sätze (wie in diesem Beispiel der Innenwinkelsummensatz von Dreiecken). Daher haben die Schülerinnen und Schüler eine überschaubare Menge an Beweismitteln zur Verfügung.
- Es lässt sich klar bestimmen, ob zwei Dreiecke kongruent zueinander sind. Somit sind alle Argumente leicht nachvollziehbar.
- Die Beweisidee lässt sich leicht und klar verbalisieren, somit können die Schülerinnen und Schüler ihre Ergebnisse gut präsentieren.
Kongruenzsätze für Vierecke
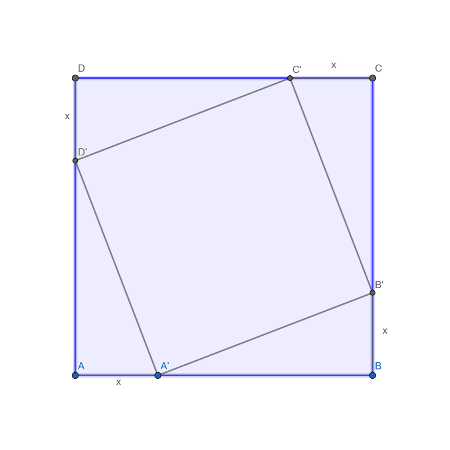
Abb. 3

Abb. 4
Für welche Werte von lässt sich ein eindeutiges Viereck konstruieren?
Für welche Werte von lassen sich zwei, nicht eindeutige Vierecke konstruieren?
Für welche Werte von lässt sich kein Viereck konstruieren?
Geometriediktate
- Eine diktierte Aussage muss von Schüler*in B geometrisch/zeichnerisch umgesetzt werden.
- Schüler*in A muss zur Entwicklung der Konstruktionsanleitung sehr genau über den Sachverhalt nachdenken. Ein Geometriediktat funktioniert nur dann gut, wenn Schüler*in A sichere Anweisungen geben kann.
- Schüler*in A muss die Anweisungen sehr präzise und genau formulieren.
- Schüler*in B muss den Anweisungen genau zuhören und sich sehr konzentrieren.