Übungen zum Strecken von Funktionsgraphen
Hole dir das Übungsblatt von deinem Lehrer.
Im Folgenden findest du Hinweise und GeoGebra Tools (mit Kurzanleitung), die du verwenden kannst, um deine Lösung zu überprüfen, oder die dir bei der Lösungsfindung helfen können. Es gibt auch kleine Zusatzaufgaben, an deren Lösung du dich wagen solltest, um dein Verständnis für den Stoff zu vertiefen.
!!! VERSUCHE ZUERST DIE AUFGABEN OHNE HILFSMITTEL UND HINWEISE ZU LÖSEN !!! -- Für Hinweise bitte weiterscrollen! --
Hinweise und Lösungen =====================================================================Aufgabe 1)
Lösung zu Teilaufgabe a):
(1) <=> (Parabel)
(2) <=> (periodische Funktion)
(3) <=> (gebrochen-rationale Funktion; Definitionslücke)
(4) <=> (Exponentialfunktion)
Hinweis zu Teilaufgabe b):
zu :
- Liegt eine Normalparabel vor?
- Öffnung
- Lage des Scheitelpunkts
zu :
- senkrechte Asymptote -> Definitionslücke
- waagrechte Asymptote -> Verschiebung in -Richtung
-
zu :
- waagrechte Asymptote von Exponentialfunktionen -> Verschiebung in -Richtung
- Spiegelung?
- Der Graph wurde in -Richtung verschoben
- Der Graph wurde nicht gestreckt
Aufgabe 2): GeoGebra (CAS)
Aufgabe 3)
Siehe Abbildungen 1 und 2 für mehr Informationen.

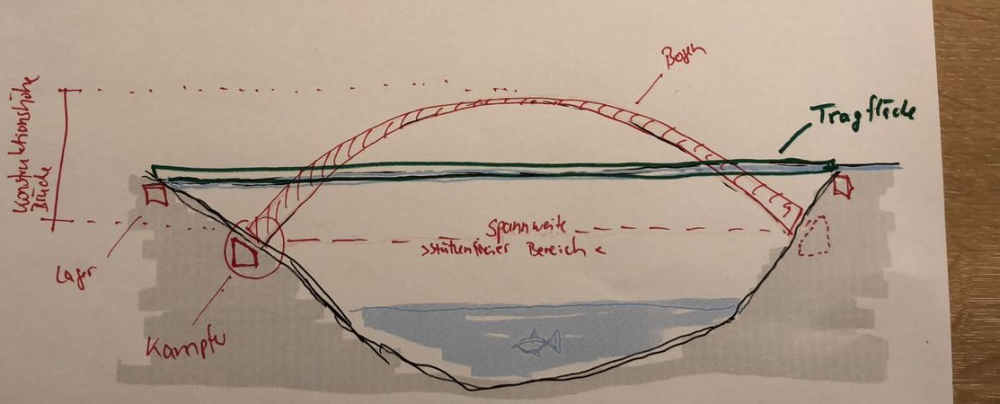
Hinweise:
zu Teilaufgabe a):
- Die Lage einer Parabel im Koordinatensystem ist nicht fest.
-> Schnittpunkte mit der x-Achse
-> Lage des Scheitelpunkts
zu Teilaufgabe b):
- vgl. Kapitel 1, Aufgabe 3
zu Teilaufgabe c) (siehe folgende GeoGebra Applets):
- Variante 1: Wähle die Kämpfer als Nullstellen der Funktion. Lege den linken Kämpfer in den Ursprung.
- Variante 2: Wähle wieder die Kämpfer als Nullstellen. Lege dieses Mal den Hochpunkt auf die y-Achse.
- Variante 3: Lege den Hochpunkt auf die y-Achse und die Tragfläche auf die x-Achse.
- Variante 4: individuelle Lösung
Variante 1
Variante 2
Variante 3
=====================================================================
=====================================================================
Du hast das Kapitel "Streckung von Funktionsgraphen" nun abgeschlossen! Super gemacht :)
===================================================================== =====================================================================