Wurzelgleichungen
Wiederholung
Terme sind sinnvolle Ausdrücke mit Zahlen, Variablen, Klammern und Symbole für mathematische Verknüpfungen.
Werden zwei Terme durch ein Gleichheitszeichen (=) verbunden, nennt man dies eine Gleichung.
Lösungen sind Zahlen, die eingesetzt in der Ausgangsgleichung, eine wahre Aussage ergeben. Man erhält sie durch Äquivalenzumformungen.
Beispiel
Löse folgende Gleichung durch Äquivalenzumformungen und mache die Probe.
3(1,6x – 1,3) + 2x = 5,3x – 8,4
(Versuche jeden Schritt der Beispiellösung nachzuvollziehen.)
Lösung

Kontrolliere das Ergebnis mit dem CAS Rechner von GeoGebra.
Schreibe in Zeile 1 und verwende den Befehl Löse(<Gleichung in x>).
Beachte: Das mathematische Komma muss als Punkt (.) eingegeben werden (wie beim GTR).
Kontrolle mithilfe CAS
Wurzelgleichungen
Gleichungen, bei denen die gesuchte Variable Teil des Radikanden ist, nennt man Wurzelgleichungen.
Wurzelziehen (Radizieren) <-> Quadrieren (Umkehroperationen)
Beispiel: Löse folgende Gleichung und mache die Probe.
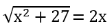
(Versuche jeden Schritt der Beispiellösung nachzuvollziehen.)
Lösung

Kontrolliere das Ergebnis mit dem CAS Rechner von GeoGebra.
Schreibe in Zeile 1 und verwende den Befehl Löse(<Gleichung in x>).
Kontrolle mithilfe CAS
Wenn a = b, dann auch a2 = b2.
Bsp. 3 = 3, dann auch 32 = 32, denn 9 = 9.
ABER
Wenn a2 = b2, dann kann auch a b sein.
Bsp. 16 = 16, könnte auch 42 = (-4)2 sein, also 4 -4
Quadrieren ist keine Äquivalenzumformung.
Merksatz

Aufgabe
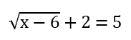
Prüfe, welche der folgenden Zahlen Lösung der Gleichung sind: x1 = 32 x2 = 15 x3 = -10
Woran erkennt man sofort, dass x3 = -10 keine Lösung der Gleichung sein kann?
Aufgabe
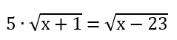
Erkläre, warum Zahlen, die kleiner als 23 sind, keine Lösung der Gleichung sein können.
Aufgabe
Löse mithilfe der Schrittfolge aus dem Merksatz folgende Wurzelgleichungen.
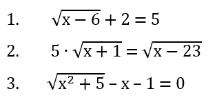
Kontrolliere die Ergebnisse mit dem CAS Rechner von GeoGebra.
Schreibe in Zeile 1 und verwende den Befehl Löse(<Gleichung in x>).
