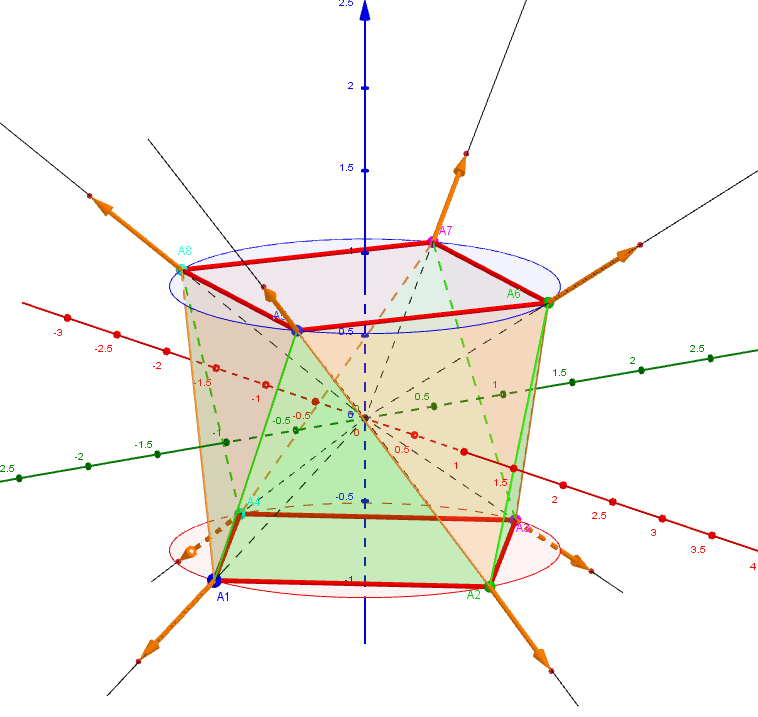
1. Acht-Punkte-Modell mit zwei Freiheitsgraden auf der Oberfläche einer Kugel
Aufgabe: Suche nach einem Algorithmus, um die gleichmäßige Verteilung der Punkte zu finden.
Suchmethode: kritische Punkte "bestimmter" funktioneller Abhängigkeiten finden und "anhand einfacher Modelle" verstehen, zu welchen teilchenverteilungen dies führt.
Als Beispiel wird ein Modell von acht Punkten auf der Oberfläche einer Kugel mit zwei Freiheitsgraden betrachtet. 8 Punkte bilden zwei parallele Quadrate. Die kann relativ zueinander drehen:
der Winkel →α x-Parameter,
der Abstand zwischen ihnen kann sich ändern:
der Neigungswinkel →θ y-Parameter.
Für bestimmte Parameterwerte können bekannte Körper erhalten werden.
Als "einige " funktionale Abhängigkeiten wählen wir die folgende Eigenschaft der geometrischen Körpern:
Gesamtabstand (Distance Sum) - die Summe der gegenseitigen Abstände aller Punktpaare auf der Kugeloberfläche.
Die Aufgabe besteht darin,
-ermitteln die Abhängigkeiten dieser Eigenschaft von den Parametern α und θ,
-herauszufinden, welche Körpern entsprechen kritischen Punkten dieser Oberfläche.
Fazit:
● Die Funktionsfläche Gesamtabstand(α, θ) (im Definitionsbereich) hat
-einen Sattelpunkt: α=0° und θ =54.73561133210024 ° -was entspricht dem Würfel (ein platonischer Körper): und
-ein lokales Maximum: α=45° und θ =55.34244880180798° -was entspricht dem quadratischen Antiprisma: (auch als Anticube bekannt).
● Jeder Punkt dieser Körper ist der geometrische Median/geometric Median und der geometrische Mittelpunkt/geometric Center (hier ist es für alle Parameterwerte!) der anderen sieben Punkte.
Hier ist eine erweiterte Version dieses Applets.
Im Applet wird noch ein weiteres Acht-Punkte-Modell mit 1 Freiheitsgrad betrachtet.
Die "resultierende Wirkung" an jedem Punkt der benachbarter Punkte.