L'iperbole come luogo geometrico
Anche l'iperbole è un luogo geometrico.
Come nel caso dell'ellisse, vengono fissati due punti detti fuochi, chiamati come al solito e . Similmente a quanto fatto per l'ellisse, considereremo innanzitutto un'iperbole riferita agli assi, cioè i cui fuochi giacciono sull'asse delle .
La caratteristica comune a tutti i punti dell'iperbole è questa: per ogni punto la differenza tra la distanza tra un fuoco e la distanza dell'altro fuoco è costante. Anche in questo caso il valore di questa costante è rappresentato dall'espressione .
Questo equivale a dire che
Da notare che in questo caso è necessario utilizzare un modulo, perché la differenza potrebbe risultare negativa.
L'iperbole è più complessa dell'ellisse, sia perché i calcoli per ottenere la sua equazione sono più complessi, sia perché la proprietà dei suoi punti non può essere interpretata in modo visivo.
Come nel caso dell'ellisse, i fuochi sono sull'asse x ed hanno coordinate e . Calcolando le espressioni contenute nella formula otterremo qualcosa di simile al caso dell'ellisse:
Dopo aver svolto i calcoli, che sono ancora più complessi anche a causa della presenza del valore assoluto, si ottiene che nel caso semplice che abbiamo scelto noi la formula dell'iperbole diventa molto semplice:
Come nel caso dell'ellisse è la quantità che compare nella definizione iniziale, mentre è legato ad ed alla distanza focale da una relazione di tipo Pitagorico, solo che in questo caso il ruolo dell'ipotenusa è svolto dalla distanza focale:
Visualizziamo tutti questi concetti nell'animazione qui sotto.
VERIFICA DELLE INTERSEZIONI
Anche se non abbiamo svolto tutti i calcoli per l'iperbole come abbiamo fatto nel caso dell'ellisse, possiamo verificare la coerenza di alcune delle caratteristiche individuate, ed in particolare le intersezioni con gli assi.
Se cerchiamo le intersezioni con l'asse delle infatti troviamo, similmente a quanto ottenuto per l'ellisse:
Quindi l'iperbole incontra l'asse nei punti e . Questi due punti sono detti vertici reali dell'iperbole.
Se invece cerchiamo le intersezioni con l'asse delle otteniamo un risultato molto diverso:
Poiché è una quantità non negativa (in realtà è sempre positiva, perché il caso non è compatibile con l'equazione dell'iperbole), è una quantità negativa, della quale quindi non è possibile estrarre la radice quadrata. Di conseguenza l'iperbole non ha intersezioni con l'asse delle , ed i punti e sono detti vertici virtuali dell'iperbole.
Il parametro non ha quindi nessun significato geometrico immediato, ma è molto utile (anche visivamente) per definire gli asintoti dell'iperbole, che approfondiremo nel prossimo paragrafo.
ASINTOTI, LIMITI E L'INFINITO
Approfondiamo il concetto di asintoto. Dal disegno nell'animazione precedente vediamo che l'iperbole sembra avvicinarsi sempre più alle rette che abbiamo tracciato, imitandone l'andamento mano a mano che si considerano valori di sempre più grandi positivi (cioè verso destra) o negativi (verso sinistra). L'immagine qui sotto utilizza una scala che mostra in modo più chiaro questo tipo di comportamento.
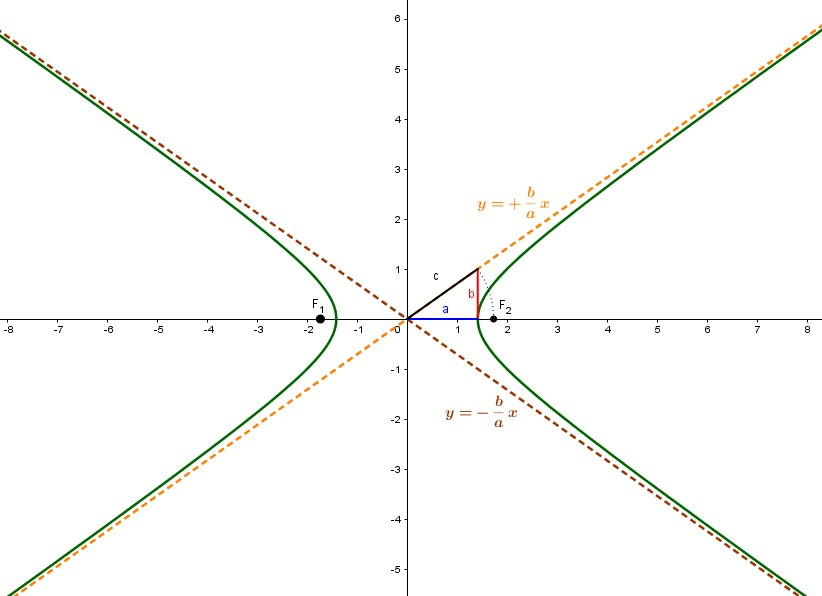
Vediamo come si comporta l'iperbole in questa parte del piano. Innanzitutto ricaviamo la dall'equazione dell'iperbole, in modo da confrontarla con quella delle rette che svolgono il ruolo di asintoto. Otteniamo:
Volendo portar fuori la (ed intanto che ci siamo anche la ) raccogliamo sotto la radice:
Abbiamo raccolto anche se il fattore non era presente in tutti i termini al radicando; possiamo verificare che eseguendo il prodotto che abbiamo creato si ottiene il radicando di partenza, e quindi le due espressioni sono equivalenti. A questo punto possiamo portare fuori il fattore prima della parentesi.
Se ora valutiamo questa espressione per valori di molto grandi (sia positivi che negativi), notiamo che al frazione che compare sotto la radice dà dei risultati sempre più piccoli: è un certo numero, comunque finito, mentre all'aumentare di il denominatore diventa un valore sempre più grande, senza limiti, e quindi la frazione dà un risultato sempre più piccolo, che tende a zero.
Il simbolo introduce il concetto di infinito, che viene definito come una quantità maggiore di qualsiasi numero sia possibile immaginare. La scrittura si legge " tende a più infinito" ed indica che stiamo considerando valori di sempre più vicini all'infinito, e quindi sempre più grandi (analogamente scrivendo indichiamo che stiamo considerando valori di negativi e sempre più grandi in valore assoluto).
La scrittura si legge "limite per che tende a più infinito di..." ed indica appunto che stiamo studiando come si comporta il risultato dell'espressione quando la valutiamo per valori di in quella zona del piano cartesiano (in questo caso per valori molto grandi).
Il limite è uno strumento dell'analisi e viene usato per calcolare il valore a cui si avvicina il risultato di una data espressione. In questo caso ci aiuta a capire che la frazione sotto la radice diventa un contributo sempre più trascurabile, mano a mano che si considerano maggiori, e quindi la radice dà un risultato sempre più simile ad , con la conseguenza che la che otteniamo diventa sempre più simile a quelle degli asintoti. Possiamo formalizzare questa descrizione con la scrittura
In questo caso abbiamo usato la scrittura in forma simbolica per indicare che la funzione, quando è considerata per molto grandi e positivi, assume un comportamento molto simile a quello degli asintoti. Abbiamo visto che le stesse considerazioni valgono quando valutiamo la funzione per valori di molto grandi e negativi, e quindi possiamo scrivere anche:
LE IPERBOLI CON FUOCHI SULL'ASSE DELLE Y
Se ripetiamo i ragionamenti visti finora ma collochiamo i fuochi sull'asse delle invece che sull'asse delle , l'equazione cambia ed il segno meno precede il termine in , diventando quindi
La relazione tra i coefficienti , e invece rimane invariata:
e la distanza focale resta quindi il valore maggiore tra i tre.
Anche le equazioni dei due asintoti rimangono identiche, come si vede nell'immagine riprodotta sotto.
![In figura è mostrato un esempio di iperbole con fuochi sull'asse [math]y[/math]. Come si vede dalla costruzione geometrica, il parametro [math]\textcolor{#007700}{c}[/math] continua a svolgere il ruolo di ipotenusa nella relazione Pitagorica tra i tre, e le equazioni dei due asintoti restano identiche (graficamente si osserva che [math]\textcolor{red}{b}[/math] continua a rappresentare la variazione sulle [math]y[/math] e [math]\textcolor{blue}{a}[/math] quella sulle [math]x[/math], quindi [math]m=\frac{\Delta y}{\Delta x} = \frac{b}{a}[/math]).
Le intersezioni invece si sono spostate dall'asse [math]x[/math] all'asse [math]y[/math], quindi il ruolo di vertici reali e virtuali sono invertiti.](https://www.geogebra.org/resource/jehybb7y/lu0NC2sV5S8W5tYe/material-jehybb7y.png)