匀变速直线运动的推论二：中间位置速度
一、中间位置速度推论
设物体以初速度，加速度做匀变速直线运动，全程运动位移为，在运动终点时的速度为。
中间位置速度，中间时刻速度，可以证明，>。
二、应用情景
中间位置速度的推论应用条件比较明显，一般只要匀变速直线运动中出现连续相等的位移，都可以想到这个推论。
例1：一段笔直的大街两侧都栽有白杨树，一侧相邻白杨树的间距均为5m，一辆摩托车可视为质点，匀加速通过这段街道，摩托车通过第一棵白杨树的速度是1m/s，通过第三棵白杨树的速度是7m/s，那么通过第二棵树时，摩托车的速度为（ ）
解析：
三棵树等间距，则第二棵白杨树为第一和第三棵白杨树的中间位置，
例2：如图所示，一小物体沿斜面向上做匀减速直线运动过程中依次经过A、C、B三点，其中C点为AB的中点，若小物体经过A、B两点时的速度分别为7m/s和1m/s。则小物体从A点运动到C点的时间与从C点运动到B点的时间之比为（ ）
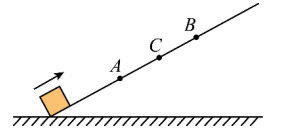
解析：
C为A、B的中间位置，
因为全程的加速度不变，且，
故，选A
| A．4m/s | B．5m/s | C．6m/s | D．7m/s |
A． | B． | C． | D． |
例3：某高速铁路的动车采取8节车厢编组。动车从某站开出时做匀加速直线运动，当车头经过路边灯箱时速度大小为
，车尾经过该灯箱时速度大小为
。每节车厢的长度相等，前后四节车厢分别经过灯箱的时间之比为（ ）
解析：
列车被分为两段相等的车厢。
第四、五节车厢的连接处为经过灯箱时的速度
因为全程的加速度不变，且，
故，选D
，车尾经过该灯箱时速度大小为。每节车厢的长度相等，前后四节车厢分别经过灯箱的时间之比为（ ）
A． | B． | C． | D． |
例4：物体做直线运动，在t时间内通过的位移为x，在中间位置处的速度为v1，对应的时候为t1，且在中间时刻处的速度为v2，则v1和v2的关系正确的是（ ）
解析：
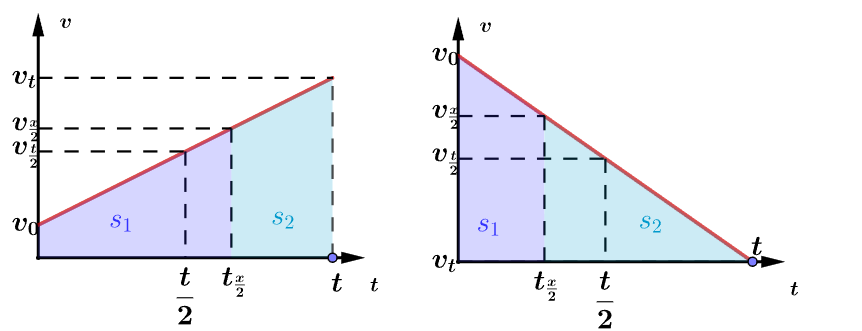从图像可以看出，选A
| A．物体做匀加速直线运动时，v1>v2，t1> |
| B．物体做匀减速直线运动时，v1>v2，t1> |
| C．物体做匀加速直线运动时，v1<v2，t1< |
| D．物体做匀减速直线运动时，v1<v2，t1> |
从图像可以看出，选A