À la recherche du coefficient (Partie I - le rayon)
Avant-propos
Nous avons donc établit expérimentalement, que l'angle est proportionnel à l'arc (et réciproquement).
Donc, pour un cercle donné, il existe un nombre fixe qui fait le lien entre l'angle au centre et la longueur de l'arc : le coefficient de proportionnalité.
Nous allons trouver ce nombre ♦.
Dans chaque angle, calcule le coefficient de proportionnalité
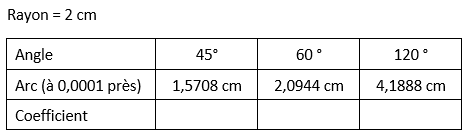
Analyse :
Comprends-tu d'où sort ce coefficient ?
Conséquence :
Nous allons devoir travailler un peu plus pour lever le voile sur le coefficient de proportionnalité qui relie angle et arc d'un cercle. Pour ce faire, nous allons étudier le rôle que joue le rayon du cercle sur la longueur de l'arc, une fois l'angle choisi.
Effet du rayon du cercle sur la longueur de l'arc
Ci-dessous, nous avons construit un cercle de rayon 1 cm ainsi que l'arc de cercle intercepté par l'angle au centre, en orange.
Puis, nous avons construit un agrandissement ou une réduction de ce cercle. L'arc en rouge est l'arc de ce cercle intercepté par le même angle au centre.
Analyse :
Après avoir choisi un angle, quand tu fais varier le facteur d'agrandissement ou de réduction, l'arc rouge est-il un agrandissement (ou une réduction) de l'arc orange ?
Pouvons-nous affirmer que la longueur de l'arc est proportionnelle au rayon* du cercle ? (* ou au diamètre, ce qui ne change pas la nature de la relation.)
Conclusion partielle
Ainsi, nous venons de voir que :
- Non seulement, la longueur de l'arc est proportionnelle à l'angle au centre,
- Mais aussi que la longueur de l'arc est proportionnelle au rayon du cercle.
Qui devient :
Il s'agit maintenant de trouver la valeur de ♥.