PROGRAM LINIER
A. KOMPETENSI DASAR
3.2 Menjelaskan program linear dua variabel dan metode penyelesaiannya dengan menggunakan masalah kontekstual.
4.2 Menyelesaikan masalah kontekstual yang berkaitan dengan program linear dua variabel.
B. INDIKATOR PENCAPAIAN KOMPETENSI
3.2.1 Menjelaskan pengertian program linear dua variabel
3.2.2 Menjelaskan sistem pertidaksamaan linier dua variabel
3.2.3 Menjelaskan nilai optimum fungsi objektif
3.2.4 Menjelaskan penerapan program liniear dua variabel dalam menyelesaikan masalah kontekstual
4.2.1 Menunjukkan variabel dari permasalahan berkaitan dengan pertidaksamaan linier dua variabel dari
permasalahan
4.2.2 Membuat model matematika program linier dua variabel dari masalah kontekstual
4.2.3 Menentukan nilai optimum sistem pertidaksamaan linier dua variabel
C. TUJUAN PEMBELAJARAN
1. Setelah kegiatan diskusi dan tanya jawab dengan geogebra melalui pembelajaran tatap muka, siswa dengan tanggung jawab dapat menjelaskan pengertian program linear dua variabel dengan benar.
2. Setelah kegiatan diskusi dan tanya jawab dengan geogebra melalui pembelajaran tatap muka, siswa dengan tanggung jawab dapat menjelaskan sistem pertidaksamaan linier dua variabel melalui kegiatan presentasi dengan benar.
3. Setelah kegiatan diskusi dan tanya jawab dengan geogebra melalui pembelajaran tatap muka, siswa dengan tanggung jawab dapat menjelaskan nilai optimum fungsi objektif dengan benar.
4. Setelah kegiatan diskusi dan tanya jawab dengan geogebra, siswa dengan tanggung jawab dapat menjelaskan penerapan program liniear dua variabel dalam menyelesaikan masalah kontekstual dengan benar.
5. Setelah kegiatan diskusi dengan geogebra melalui pembelajaran tatap muka, siswa dengan tanggung jawab dapat menunjukkan variabel dari permasalahan berkaitan dengan pertidaksamaan linier dua
variabel dari permasalahan dengan benar.
6. Melalui kegiatan diskusi siswa dengan tanggung jawab dapat membuat model matematika program linier dua variabel dari masalah kontekstual dengan benar.
7. Melalui kegiatan diskusi siswa dengan tanggung jawab dapat menentukan nilai optimum sistem
pertidaksamaan linier dua variabel dengan benar.
D. MATERI
Program linear adalah suatu metode penentuan nilai optimum dari suatu persoalan linear. Nilai optimum (maksimal atau minimum) diperoleh dari nilai dalam suatu himpunan penyelesaiaan persoalan linear. Di dalam persoalan linear terdapat fungsi linear yang bisa disebut sebagai fungsi objektif. Persyaratan, batasan, dan kendala dalam persoalan linear merupakan sistem pertidaksamaan linear.

Pertidaksamaan linear dua variabel
Pertidaksamaan linear dua variabel merupakan bentuk pertidaksamaan dengan memuat dua peubah (variabel) dengan pangkat tertingginya adalah satu (linear).
Bentuk umum dari pertidaksamaan linear dua variabel yaitu,
a1x + b1y = c1
a2x + b2y = c2
Model Matematika
Persoalan dalam program linear yang masih dinyatakan dalam kalimat-kalimat pernyataan umum, kemudian diubah kedalam model matematika. Model matematika merupakan pernyataan yang menggunakan peubah dan notasi matematika.
Nilai Optimum Fungsi Objektif
Fungsi objektif merupakan fungsi linear dan batasan-batasan pertidaksamaan linear yang memiliki himpunan penyelesaian. Himpunan penyelesaian yang ada merupakan titik-titik dalam diagram cartesius yang jika koordinatnya disubstitusikan kedalam fungsi linear dapat memenuhi persyaratan yang ditentukan.
Nilai optimum fungsi objektif dari suatu persoalan linear dapat ditentukan dengan metode grafik. Dengan melihat grafik dari fungsi objektif dan batasan-batasannya dapat ditentukan letak titik yang menjadi nilai optimum. Langkah-langkahnya sebagai berikut :
- Menggambar himpunan penyelesaian dari semua batasan syarat yang ada di cartesius.
- Menentukan titik-titik ekstrim yang merupakan perpotongan garis batasan dengan garis batasan yang lainnya. Titik-titik ekstrim tersebut merupakan himpunan penyelesaian dari batasannya dan memiliki kemungkinan besar membuat fungsi menjadi optimum.
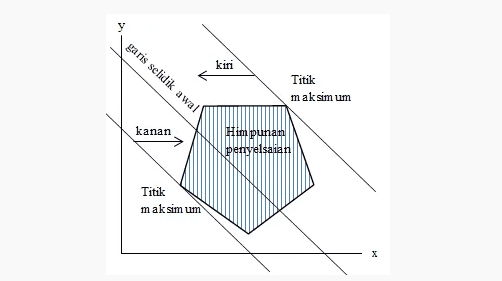
- Menyelidiki nilai optimum fungsi objektif dengan dua acara yaitu :
- Jika maksimum, maka dibuat garis yang sejajar garis selidik awal sehingga membuat himpunan penyelesaian berada di kiri garis tersebut. Titik yang dilalui garis tersebut adalah titik maksimum.
- Jika minimum, maka dibuat garis yang sejajar garis selidik awal sehingga membuat himpunan penyelesaian berada di kanan garis tersebut. Titik yang dilalui garis tersebut adalah titik minimum.
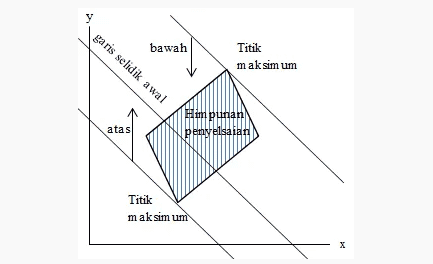
Cara 2 (syarat b > 0)
- Jika maksimum, maka dibuat garis yang sejajar garis selidik awal sehingga membuat himpunan penyelesaian berada di bawah garis tersebut. Titik yang dilalui garis tersebut adalah titik maksimum.
- Jika minimum, maka dibuat garis yang sejajar garis selidik awal sehingga membuat himpunan penyelesaian berada di atas garis tersebut. Titik yang dilalui garis tersebut adalah titik minimum.
Membandingkan Nilai Fungsi Tiap Titik Ekstrim
Menyelidiki nilai optimum dari fungsi objektif juga dapat dilakukan dengan terlebih dahulu menentukan titik-titik potong dari garis-garis batas yang ada. Titik-titip potong tersebut merupakan nilai ekstrim yang berpotensi memiliki nilai maksimum di salah satu titiknya.
Berdasarkan titik-titik tersebut ditentukan nilai masing-masing fungsinya, kemudian dibandingkan. Nilai terbesar merupakan nilai maksimum dan nilai terkecil merupakan nilai minimum.
E. SIMULASI
Simulasi Menggunakan Geogebra
Simulasi Cara Menentukan Pertidaksamaan Linear
Simulasi Cara Menentukan Model Matematika
Simulasi Cara Menentukan Nilai Optimum
F. LATIHAN SOAL
Berisi soal-soal latihan dengan geogebra