Lage von Geraden
Mögliche Lage von Geraden
Auf dem Applet unten sehen Sie zwei sich im Raum schneidende Geraden. a) Welche weiteren Möglichkeiten für die Lage von Geraden gibt es? b) Was gilt für die Richtungsvektoren in diesen Fällen
Verfahren zur Bestimmung der gegenseitigen Lage von Geraden
Sind die Gleichungen zweier Geraden g und h gegeben und die Frage ihrer gegenseitigen Lage zu klären folgt daraus direkt die Art des Vorgehens:
1. Geradengleichungen gleichsetzen
2. Daraus resultirendes LGS mit 3 Gleichungen (je 1 pro Dimension) und 2 Unbekannten (den Parametern r und s) lösen
3. Ergebnis analysieren:
a) unendlich viele Lösungen: Geraden sind identisch, fallen ineinander, die beiden Gleichungen sind Darstellungen der gleichen Geraden.
b) eine Lösung: Die Geraden schneiden sich. Schnittpunkt kann durch einsetzen eines der beiden Parameter in die entsprechende Gleichung bestimmt und durch einsetzen des anderen Parameters in die je andere Gleichung geprüft werden.
c) keine Lösung:
i) Richgungsvektoren parallel --> Geraden sind parallel
ii) Richgungsvektoren nicht parallel --> Geraden sind windschief
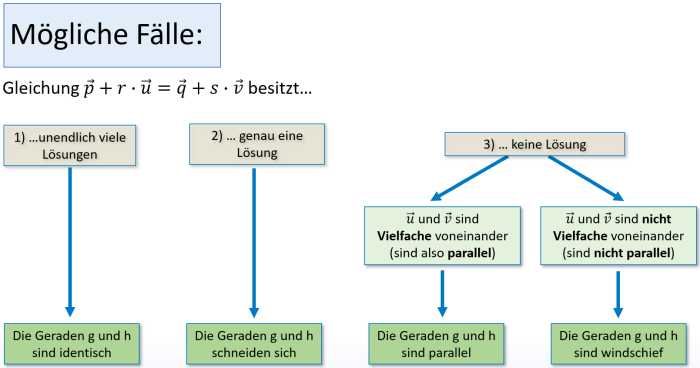
Damit ergibt sich für die möglichen Fälle für die gegenseitige Lage von Geraden: