IM3.7.2 Two way tables (TWT)
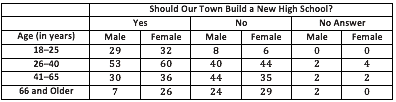
1. Based on this survey, do you think the school board should recommend building a new high school? Explain your answer. 2. An eligible voter is picked at random. If this person is 21 years old, do you think he would indicate that the town should build a high school? Why or why not? 3. An eligible voter is picked at random. If this person is 55 years old, do you think she would indicate that the town should build a high school? Why or why not? 4. The school board wondered if the probability of recommending a new high school was different for different age categories. Why do you think the survey classified voters using the age categories 18–25 years old, 26–40years old, 41–65years old, and 66 years old and older?
Make a TWT
Critiquing the reasoning of others
6. A local news service plans to write an article summarizing the survey results. Three possible headlines for this article are provided below. Is each headline accurate or inaccurate? Support your answer using probabilities calculated using the table above. Headline 1: Waldo Voters Likely to Support Building a New High School Headline 2: Older Voters Less Likely to Support Building a New High School Headline 3: Younger Voters Not Interested in Building a New High School
Using probability to make decisions
7. The school board decided to put the decision on whether or not to build the high school up for a referendum in the next election. At the last referendum regarding this issue, only 25 of the eligible voters ages 18–25 voted, 110 of the eligible voters ages 26–40 voted, 130 of the eligible voters ages 41–65 voted, and 80 of the eligible voters ages 66 and older voted. If the voters in the next election turn out in similar numbers, do you think this referendum will pass? Justify your answer. 8. Is it possible that your prediction of the election outcome might be incorrect? Explain.