B. Bisectrices e incentro
Construcción
1. Traza una circunferencia de centro en el vértice del ángulo y de radio cualquiera (suficientemente grande). 
2. Halla la intersección de la circunferencia anterior con los lados del ángulo. 
3. Traza una circunferencia con centro en uno de los puntos de intersección anterior y de radio cualquiera (suficientemente grande).
4. Desde el otro punto de intersección traza una circunferencia con el mismo radio, utiliza para ello la herramienta "compás" seleccionando primero la longitud del radio.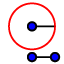 
5. Halla el punto de intersección de las dos circunferencias .
6. Traza la recta que pasa por el vértice A y por el punto anterior. 
ESTA ES LA BISECTRIZ DEL ÁNGULO.
7. Oculta todas las construcciones auxiliares (circunferencias, puntos...) y quédate solo con la construcción original y la bisectriz.
8. Cambia el formato de la bisectriz: llámala "BISECTRIZ", cambia su color y su grosor.
9. Elige un punto de la bisectriz. 
10. Traza las perpendiculares desde ese punto a ambos lados del triángulo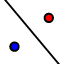 
y halla los puntos de intersección con los lados . Oculta las perpendiculares y traza segmentos desde le punto elegido a los puntos de intersección. 
11. Mide la longitud de estos segmentos 
, prueba a mover el punto 
y observa lo que ocurre.
2. Halla la intersección de la circunferencia anterior con los lados del ángulo.
3. Traza una circunferencia con centro en uno de los puntos de intersección anterior y de radio cualquiera (suficientemente grande).
4. Desde el otro punto de intersección traza una circunferencia con el mismo radio, utiliza para ello la herramienta "compás" seleccionando primero la longitud del radio.
5. Halla el punto de intersección de las dos circunferencias .
6. Traza la recta que pasa por el vértice A y por el punto anterior.
ESTA ES LA BISECTRIZ DEL ÁNGULO.
7. Oculta todas las construcciones auxiliares (circunferencias, puntos...) y quédate solo con la construcción original y la bisectriz.
8. Cambia el formato de la bisectriz: llámala "BISECTRIZ", cambia su color y su grosor.
9. Elige un punto de la bisectriz.
10. Traza las perpendiculares desde ese punto a ambos lados del triángulo y halla los puntos de intersección con los lados . Oculta las perpendiculares y traza segmentos desde le punto elegido a los puntos de intersección.
11. Mide la longitud de estos segmentos , prueba a mover el punto y observa lo que ocurre.
Construcción (de las bisectrices y el incentro de un triángulo)
1. Hallas las bisectrices de cada uno de los ángulos del triángulo (tienes que seleccionar tres puntos: punto lateral-vértice-punto lateral).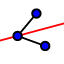
2. Halla la intersección de dos de las bisectrices y comprueba que el punto de intersección (el INCENTRO) es el punto de corte de las tres.
3. Traza una perpendicular desde el incentro a uno de los lados y obtén el punto de intersección con el lado .
4. Traza una circunferencia con centro en el incentro y de radio hasta el punto anterior.
ESTA ES LA CIRCUNFERENCIA INSCRITA.
5. Halla los otros puntos de tangencia: la perpendicular desde el incentro a los otros dos lados y la intersección entre la perpendicular y el lado. Después mide la distancia desde el centro a cada punto de tangencial.
6. Mueve los vértices del triángulo y observa ¿se sale el incentro en algún momento del triángulo?
2. Halla la intersección de dos de las bisectrices y comprueba que el punto de intersección (el INCENTRO) es el punto de corte de las tres.
3. Traza una perpendicular desde el incentro a uno de los lados y obtén el punto de intersección con el lado .
4. Traza una circunferencia con centro en el incentro y de radio hasta el punto anterior.
ESTA ES LA CIRCUNFERENCIA INSCRITA.
5. Halla los otros puntos de tangencia: la perpendicular desde el incentro a los otros dos lados y la intersección entre la perpendicular y el lado. Después mide la distancia desde el centro a cada punto de tangencial.
6. Mueve los vértices del triángulo y observa ¿se sale el incentro en algún momento del triángulo?