Ciclo trigonométrico
Definição
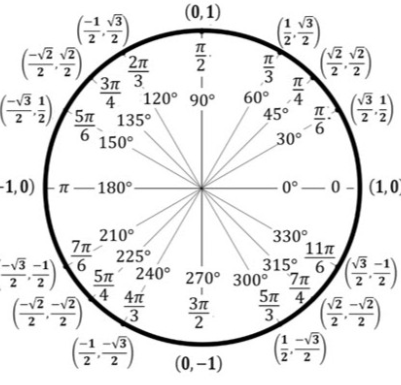
O ciclo trigonométrico é uma representação gráfica das funções trigonométricas no plano cartesiano, onde o círculo unitário (um círculo com raio 1) é utilizado para ilustrar como as funções seno, cosseno e tangente variam à medida que o ângulo (θ) aumenta. Ele é uma ferramenta essencial para entender essas funções de maneira visual e intuitiva.
Características
- O ciclo trigonométrico é representado por um círculo unitário, que tem raio igual a 1 e centro na origem do plano cartesiano, ou seja, no ponto (0,0).
- O círculo é desenhado no plano xy onde o eixo x é o eixo dos valores de cosseno e o eixo y é o eixo dos valores de seno.
- À medida que o ângulo θ (em radianos) aumenta, o ponto de interseção da linha de ângulo com a circunferência do círculo se move no sentido anti-horário.
- A cada volta completa (ou ciclo), o ângulo θ percorre um valor de 2π radianos (360 graus).
- Cosseno (cos(θ)): O valor do cosseno de um ângulo é dado pela coordenada x do ponto de interseção da linha de ângulo com o círculo unitário.
- Seno (sin(θ)): O valor do seno de um ângulo é dado pela coordenada y do ponto de interseção da linha de ângulo com o círculo unitário.
- Em outras palavras:
- cos(θ)=x
- sin(θ)=y
- Em outras palavras: