Google Classroom - Interaktiva lektioner
GeoGebraGeoGebra Classroom - Interaktiva lektioner
GeoGebra

Area of Parallelogram (13-3)

Författare/skapare:Lily, Tim Brzezinski, Vincent Pantaloni, Duane Habecker

Formula

The formula we use to find the area of a parallelogram is the same as the formula we use to find the area of a rectangle:
This is because we can reconstruct a parallelogram to form a rectangle with the same area.

Let’s take a closer look...

Try to count the number of squares inside this pink and purple parallelogram below. How many squares (i.e. square units) do you estimate to be inside this parallelogram?

Drag the green slider to see the animation. Observe what happens. What shape do you see now?

How many squares do you now count in the newer shape that was formed?

How does the area of this new shape compare with the area of the original parallelogram?

Välj alla som är tillämpliga
  • A
  • B
  • C
Kontrollera svaret (3)

Watch this video to see some examples using the formula

True or False

The formula to find the area of a parallelogram is the same as the formula to find the area of a rectangle.

Välj alla som är tillämpliga
  • A
  • B
Kontrollera svaret (3)

The formula to find the area of a parallelogram is

Välj alla som är tillämpliga
  • A
  • B
  • C
Kontrollera svaret (3)
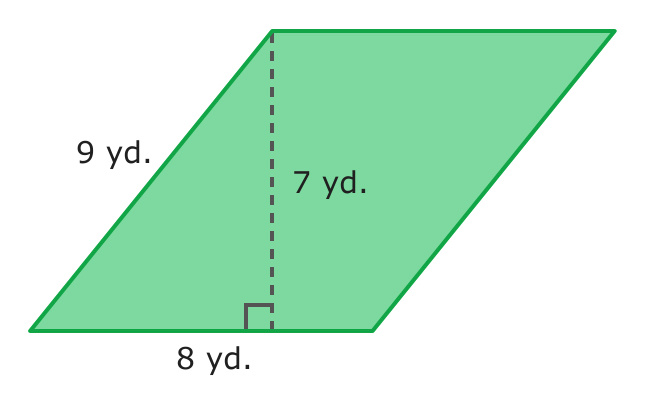
Image

Which is the height in the parallelogram above?

Välj alla som är tillämpliga
  • A
  • B
  • C
Kontrollera svaret (3)
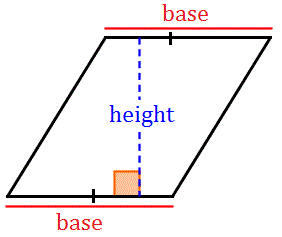
Image

Which are always true about the height of a parallelogram?

Välj alla som är tillämpliga
  • A
  • B
  • C
  • D
  • E
Kontrollera svaret (3)

Formula

Area = Base x Height

Practice

Practice

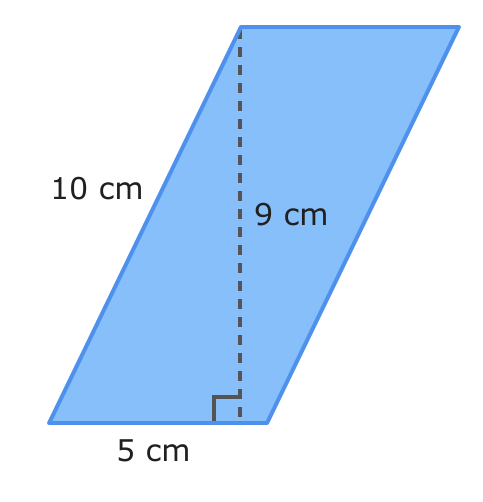
What is the area of this parallelogram?

Välj alla som är tillämpliga
  • A
  • B
  • C
  • D
Kontrollera svaret (3)

Area is always measured in

Välj alla som är tillämpliga
  • A
  • B
Kontrollera svaret (3)
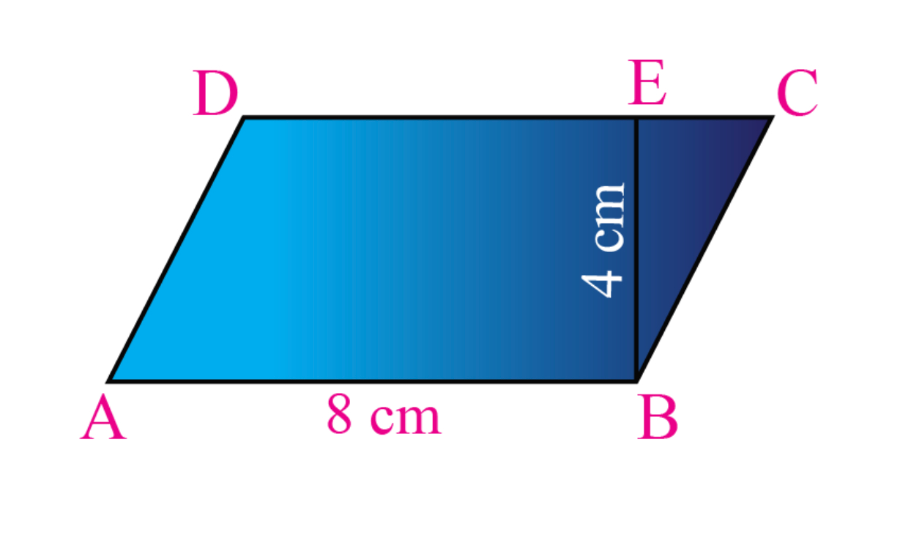
Image

What is the area of this parallelogram?

Nya resurser

Upptäck resurser

Undersök matematisk områden