Запремина обртног тела
ПРИМЕНА ОДРЕЂЕНОГ ИНТЕГРАЛА У ИЗРАЧУНАВАЊУ ЗАПРЕМИНЕ
Нека је функција у=f(x) дефинисана, непрекидна и f(x) на [a,b]. Tада је запремина обртног тела насталог ротацијом око х-осе криволинијског трапеза одређеног функцијом у=f(x) на [a,b] једнака
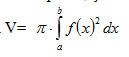
Ако је потребно израчунати запремину обртног тела насталог ротацијом око х-осе равни између две функције у=f(x) и у= g(x), нађу се прве координате пресечних тачака х1 и х2 а затим се рачуна
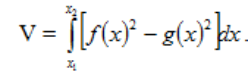
Пример
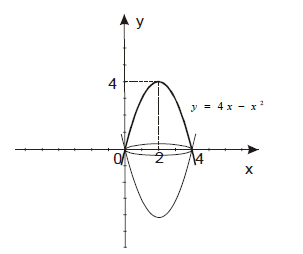
Одредити запремину тела које настаје ротацијом око Ox-осе дела површи ограниченог кривом y=4x-x2