Parabelgleichung zu einem Punkt bestimmen
Wiederholung: Punktprobe
Um die Funktionsgleichung zu einem gegebenen Punkt zu bestimmen, benötigst du als Grundwissen die Punktprobe.
Das hast du schon mit der Normalparabel geübt, indem du die x-Koordinate eines Punktes in die Gleichung eingesetzt und den passenden Wert für y berechnet hast.
Das Ergebnis für vergleichst du anschließend mit der -Koordinate des Punktes. Stimmen beide überein, liegt der Punkt auf dem Graphen der Normalparabel.
Wiederholung: Punktprobe bei der Normalparabel
Kreuze die Punkte an, die auf dem Graphen der Normalparabel liegen.
Jetzt umgekehrt...
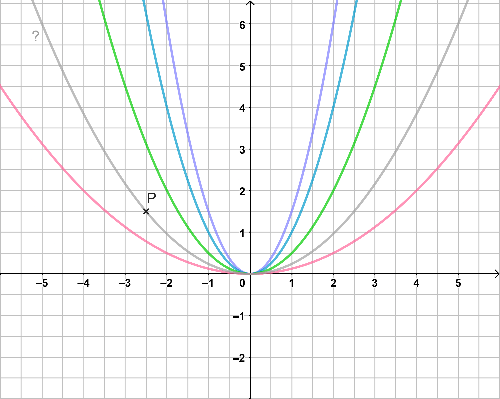
Du möchtest die passende Parabelgleichung der Form zu einem gegebenen Punkt, z.B.: .
Dann verwendest du die Punktprobe umgekehrt: Du setzt die x- und y-Koordinate in die Parabelgleichung ein. Dann löst du nach a auf. Für :
Also lautet die passende Funktionsgleichung:
Hast du's gecheckt?
Bestimme die Gleichung der Form der Parabel, auf der der Punkt liegt.

HALT! Noch nicht weiter!
Bearbeite jetzt Aufgabe 2 auf der Rückseite des Merkaufschriebs.