Estudio analítico de las cónicas en el plano.
ECUACIÓN ALGEBRAICA DE UNA CÓNICA.
Una curva cónica C, en el plano XY, satisface una ecuación algebraica de grado dos respecto a las variables x e y. Por tanto su ecuación será de la forma:
Siendo A, B, C, D, E y F números reales.
También podemos expresar la ecuación de la cónica C, en forma matricial de la forma:
Siendo M una matriz cuadrada real de orden 3 y simétrica . M se denomina matriz de coordenadas.
MATRIZ DE COORDENADAS.
EJEMPLOS.
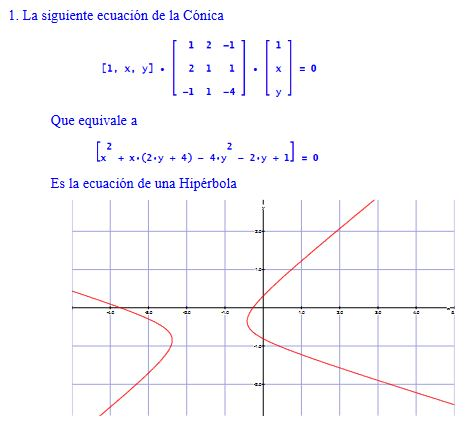
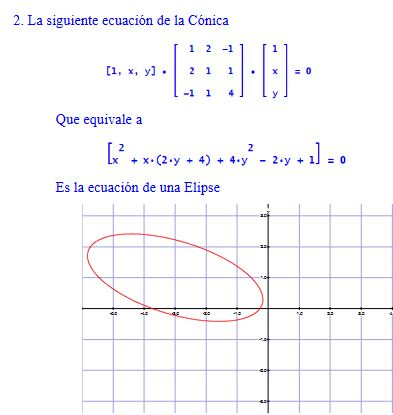
ECUACIÓN ALGEBRAICA DE LA CÓNICA.
Observaciónes:
1.- Decimos que dos puntos del plano son conjugados respecto de la cónica si se cumple: .
Si se cumple: , decimos que el punto es autoconjugado respecto de la cónica C. Es evidente que si el punto pertenece a la cónica C, entonces es autoconjugado
2.- Hay que observar que una cónica C, verifica infinitas ecuaciones de la forma , ya que si N es una matriz proporcional a M, existe un real c no nulo, tal que se verifica:
3.- Si es la ecuación de una cónica, respecto de un sistema de referencia R, y S es otro sistema de referencia, cuyas ecuaciones de cambio viene dadas por , entonces, la cónica C, respecto del nuevo sistema de referencia S vendrá dado por las ecuaciones :
EJEMPLOS.


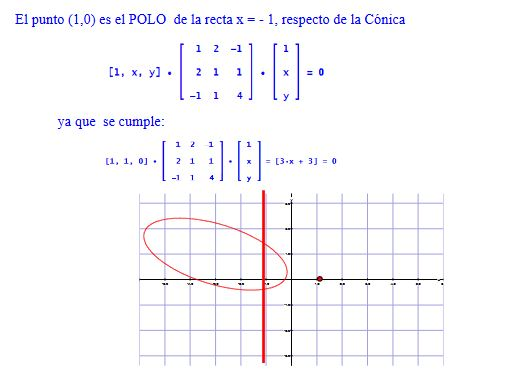
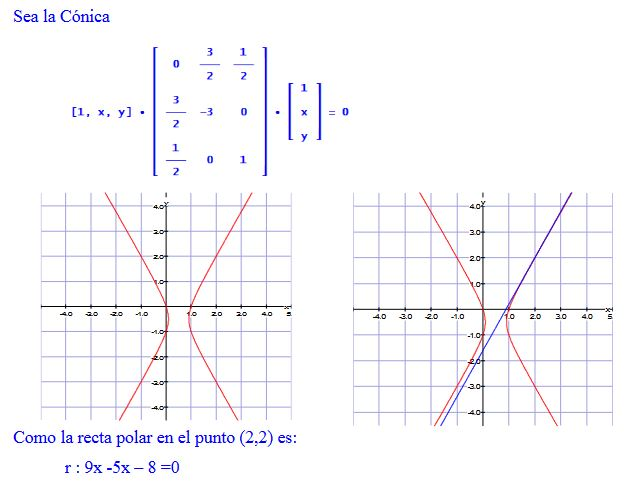
RECTA POLAR
Si es un punto del plano afín, denominamos recta polar de , respecto de la cónica
a la recta
RECTA POLAR.
Observaciones:
1.- Si No existe ningún punto P del plano afín conjugado con .
2.- Si Cualquier punto P del plano afín es conjugado con .
PUNTOS SINGULARES
El conjunto de los puntos singulares de la cónica es:
.
Es decir, dichos puntos resultan de resolver el sistema de ecuaciones:
Además, teniendo en cuenta la compatibilidad de dicho sistema se cumplirá:
- Si rango(M)=3, C no tiene puntos singulares.
- Si rango(M)=2, existe un único punto singular.
- Si rango(M)=1, existe infinitos puntos singulares (pertenecientes a una recta).
EJEMPLO.

PUNTOS SINGULARES DE UNA CÓNICA C.
Observaciones:
- La cónica es regular si , en otro caso es degenerada.
- Si la cónica C es regular y r es una recta polar del punto , entonces es único y se denomina polo de la recta r.
EJEMPLOS.
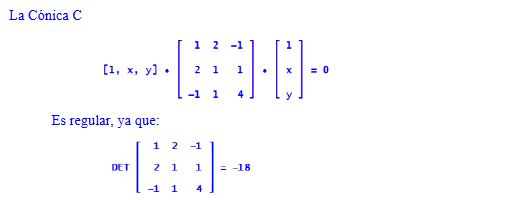
POSICIÓN DE RECTA Y CÓNICA
Si r es una recta y C una cónica, los puntos de intersección , se obtendrán al resolver el sistema de ecuaciones de la recta r y de la cónica C. Y se cumplirá:
- Si es un sistema incompatible, la recta r será exterior a la cónica C.
- Si es un sistema compatible determinado:
* Si tiene solución única r es tangente a C
* Si tiene dos soluciones r es secante a C.
- Si C es compatible indeterminado r esta incluida en C, y r es generatriz de C.
Ejemplo
Observaciones:
1.- Si la cónica C posee una recta generatriz, entonces C es unión de dos rectas del plano afín.
2.- Si C es una cónica y es un punto singular de C, entonces, toda recta que pasa por o es recta tangente a C o es recta generatriz de C.
CÓNICAS REGULARES
Si es una CÓNICA REGULAR es decir si |M| ≠ 0.
Si denominamos:
Resolviendo el sistema (1,x,y).M = (λ,0,0) ; λ ∈ R - {0}, se cumple:
a) Si , existe un único punto Q que es centro de la cónica C.
b) Si , entonces la cónica C no tiene centro, ya el sistema (1,x,y).M = (λ,0,0) ; λ ∈ R - {0}, sería incompatible.
CENTRO DE UNA CÓNICA
Un punto P ∈ A (plano afín) es CENTRO de la CÓNICA C, cuando no existe ningún punto P ' conjugado con P, respecto de la cónica C.
Como los puntos P ∈ A (plano afín), que no poseen puntos conjugados deben de cumplir la ecuación:
(1,x,y).M = (λ,0,0) ; λ ∈ R - {0}
Es equivalente a resolver el sistema de ecuaciones:
Ejemplo:
Dada la cónica:
Resolviendo las ecuaciones:
Obtenemos el Centro de la elipse (-3,1).
CÓNICAS DEGENERADAS
Si es una cónica degenerada, es decir , resolviendo el sistema:
(1,x,y).M = (λ,0,0) ; λ ∈ R - {0}
y teniendo en cuenta que para que exista solución, se tiene que cumplir:
a) Si , el sistema no tiene solución y C no tiene centro.
b) Si , y
- Si C no tiene centro.
- Si Si rango(M)=1, C no tiene centro y si rango(M)=2, el centro de C es una recta.
RECTA TANGENTE A CÓNICA Y HAZ DE CÓNICAS.
