Valor Absoluto
1.5 Valor absoluto
Introducción
Las matemáticas requieren atención con la dimensión y el valor del signo.
No es lo mismo -10 que 10, o sumar 3 + 7 que 3 + (-7).
Pero hay circunstancias en las que el signo no es determinante. Por ejemplo, en una larga caminata por el campo, el tiempo que tardes no importa si vas hacia el norte o hacia el sur. La dirección no importa, sólo la distancia.
En matemáticas, hay un concepto para tratar con situaciones donde la magnitud importa más que el signo. Se llama valor absoluto. El valor absoluto de un número consiste en su valor, sin importar su signo.
Teoría
El valor absoluto de un número entero es el número natural que resulta al suprimir su signo. El valor absoluto se escribe entre barras verticales. Valor absoluto de un número real a, se escribe |a|, es el mismo número a cuando es positivo, y opuesto de a, si a es negativo.
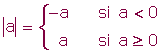
Propiedades del valor absoluto
1. El mismo número opuesto en la recta numérica tiene el mismo valor absoluto.
2. El valor absoluto de un producto es igual al producto de los valores absolutos de los factores.
3. El valor absoluto de una suma es menor o igual que la suma de los valores absolutos de los sumandos. Recordando que la definición del valor absoluto surge de nociones geométricas, y se relaciona con los conceptos de longitud y distancia.
La función de valor absoluto tiene por ecuación f(x) = |x|, y siempre representa distancias; por lo tanto, siempre será positiva o nula.
En esta condición, de ser siempre positiva o nula, su gráfica no se encontrará jamás debajo del eje x. Su gráfica va a estar siempre por encima de dicho eje o, a lo sumo, tocándolo.
Las funciones en valor absoluto siempre representan una distancia o intervalos (tramos o trozos) y se pueden resolver o calcular siguiendo los siguientes pasos:
1. Se iguala a cero la función, sin el valor absoluto, y se calculan sus raíces (los valores de x).
2. Se forman intervalos con las raíces (los valores de x) y se evalúa el signo de cada
intervalo.
3. Definimos la función a intervalos, teniendo en cuenta que en los intervalos donde la x es negativa se
cambia el signo de la función.
4. Representamos la función resultante.
Supuesto de aplicación
Ejemplo:
Calcular el valor absoluto de la función:
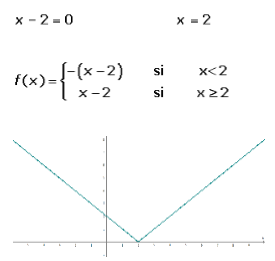
f(x) = |x − 2|
Resolución:
Algunas aplicaciones que se le dan al valor absoluto son:
- Valores existentes entre 2 números.
- Saber una distancia a recorrer en un viaje sin importar la dirección.
- Para hallar el intervalo de una temperatura. Entre cuantos grados centígrados hace reacción cierto objeto.
- Capacidades volumétricas de un objeto.
¿Qué podemos ver en el applet?
En el applet se observa que mientras el deslizador de la función avanza, existe una línea azul y gris que refleja en el eje de las x y de las y la ubicación del punto, esto se traduce al dominio y contradominio
de una función con valor absoluto.
El dominio de cualquier f(x), son los valores que puede tomar para que ésta exista, en valores absolutos el dominio puede tomar cualquier valor, es decir, todos los reales (R) (mientras no exista alguna discontinuidad).
El rango, por otro lado es aquel valor que devuelve una función, en los absolutos, solo positivos. (R+).
Dominio, mostrado por el punto color verde∴ el dominio va a se de -∞ a ∞
Rango, mostrado por el punto color azul ∴ va a ser del 0 al ∞
Función, mostrada por la línea color naranja
¿Cómo funciona?
Incluye un deslizador que permite mover la función por todo el intervalo