LÍNEAS Y PUNTOS NOTABLES EN UN TRIÁNGULO.
PENSAMIENTO Y ESTÁNDAR BÁSICO A DESARROLLAR.
- PENSAMIENTO MATEMÁTICO: Pensamiento espacial y geométrico.
- ESTÁNDAR BÁSICO DE COMPETENCIA MATEMÁTICA: Usar representaciones geométricas para resolver y formular problemas en la matemática y otras disciplinas.
PROPÓSITO DE APRENDIZAJE.
- Que el estudiante aprenda a identificar y trazar las rectas notables en el triángulo así como sus puntos de intersección.
CONCEPTOS A TENER EN CUENTA.
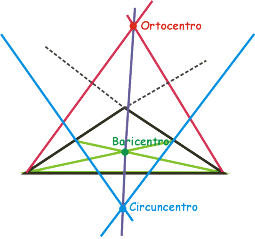
La recta que contiene los puntos notables ortocentro, baricentro y circuncentro se conoce como "Recta de Euler". Se denomina así, en honor al matemático suizo Leonhard Euler, quien en 1765 demostró la colinealidad entre estos tres puntos.
ALTURAS Y ORTOCENTRO.
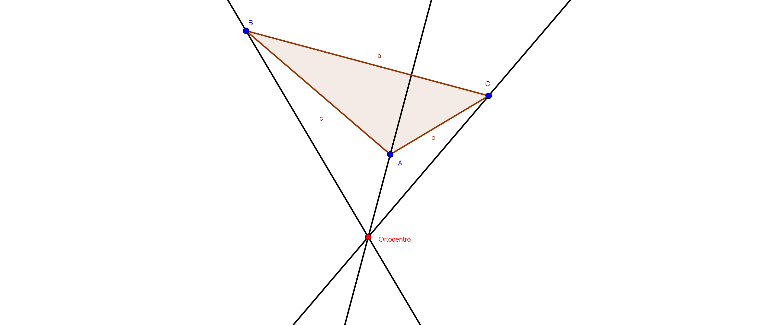
ORIENTACIONES PARA LA CONSTRUCCIÓN DE LAS ALTURAS EN UN TRIÁNGULO.
ACTIVIDAD DE APRENDIZAJE.
).
Paso 3: Pique sobre el vértice C del triángulo y muévalo a cualquier lugar de la ventana de trabajo.
Paso 4: Observe y analice qué ocurre con la posición de la altura del triángulo y con la medida de los ángulos A, B y C del triángulo.Escriba sus conclusiones. Trate de ser muy explícito en su apreciación.
Paso 5: Mueva el vértice C hasta que la altura coincida, o con el lado BC o con el lado AC. ¿Según la medida de sus ángulos, qué clase de triángulo se forma?
Paso 6: Con la herramienta "elige y mueve" (), cambie la posición de los vértices A y B del triángulo.
Paso 7: Mueva el punto C hasta que la altura coincida, o con el lado BC o con el lado AC.
¿Según la medida de sus ángulos, qué clase de triángulo se forma?
Paso 3: Mueva el vértice C hasta que la altura quede por fuera del triángulo y a la derecha del punto B. ¿Qué clase de ángulo queda, en el vértice B y en el vértice A?
Paso 4: Mueva el vértice C hasta que la altura quede por fuera del triángulo y a la izquierda del punto A. ¿Qué clase de ángulo queda, en el vértice A y en el vértice B?
Escriba, qué concluye de la posición de la altura C al lado AB, según que el ángulo A o el ángulo B sea agudo, obtuso o recto.
(Punto) y en el menú que se despliega pique en 
(Medio o Centro).
Paso 3: Pique luego sobre el lado AB del triángulo. De esta manera ubicamos el punto medio del lado AB.
Paso 4: Haga click derecho sobre el punto medio y escoja la opción "Etiqueta visible". Aparece entonces el punto D.
Paso 5: Trace la altura desde el vértice C al lado opuesto AB.
Paso 6: Con la herramienta "Elige y mueve" desplace la altura hasta que coincida con el punto medio D.a) ¿Según la medida de sus lados, qué clase de triángulo, se forma?
b) Según la medida de los ángulos, ¿Qué clase de ángulos son, el ángulo A y el ángulo B?
OTRA DEFINICIÓN DE ALTURA.
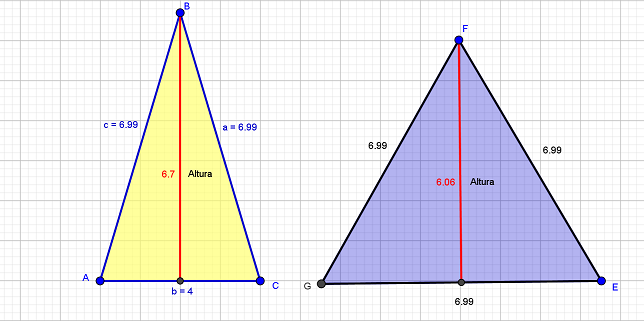
¿Con base en lo enunciado anteriormente, qué procedimiento matemático o teorema por usted conocido permite calcular el valor de la altura del triángulo formado?
Observa y analice el resultado de la construcción y escriba sus conclusiones.
APLICACIONES REALES.
TAREA DE INVESTIGACIÓN.
Una de las situaciones reales que inquietaron al hombre desde hace cientos de años, fue el problema de medir y calcular el área y el perímetros de diversas formas geométricas. Para el caso que hemos trabajado, que son los triángulos, existen formas matemáticas de determinar estos parámetros con base por ejemplo en el cálculo de las alturas de un triángulo.
Como complemento a lo tratado en el tema de clase:
- Consulte qué procedimientos o formas matemáticas son las más conocidas para determinar o calcular analíticamente las alturas de un triángulo.
En su cuaderno de notas, escriba mínimo dos hojas, sobre la biografía de dos de los matemáticos más importantes que hayan aportado significativamente a la solución del problema planteado.
AUTOEVALUACIÓN.
Apreciado estudiante. Redacte de manera breve y concisa que aprendió, qué dificultades se le presentaron y que acciones propone para superarlas. Si tiene sugerencias, no dude en hacerlas.