A Thalesz tétel alkalmazása
| 1. példa Szerkesszünk adott körhöz adott külső pontra illeszkedő érintőt. |
Megoldás
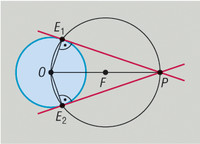
Mivel az érintési pontba húzott sugár merőleges az érintőre, azért Thalész tételéből adódóan a kör O középpontját az adott P külső ponttal összekötő szakasz mint átmérő fölé rajzolt kör metszi ki az érintési pontot az adott körből.
Mivel az OP szakasz fölé írt Thalész-kör két pontban metszi az adott kört, ezért két megfelelő érintőt kapunk.
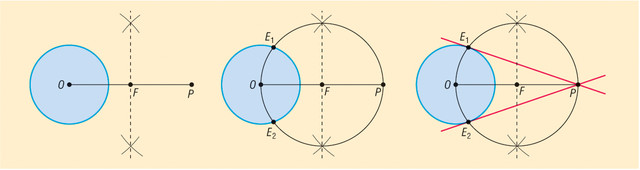
A szerkesztés menete:
|
| Tétel: A körhöz külső pontból húzott érintőszakaszok egyenlő hosszúak. |
2. példa
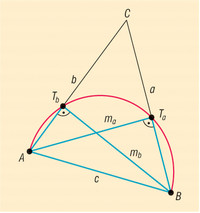
Bizonyítsuk be, hogy a háromszög egy oldalának két végpontja és az ezekből induló magasságok talppontjai egy körre illeszkednek.
Megoldás
Emlékeztetünk arra, hogy a háromszög magasságának talppontja a magasságvonal és a megfelelő oldal egyenesének metszéspontja.
Az ABT a és ABT b háromszögek olyan derékszögű háromszögek, amelyeknek közös átfogója a háromszög AB oldala. Ezen két derékszögű háromszög körülírt köre Thalész tételének megfordításából adódóan ugyanaz a kör, nevezetesen az AB oldal mint átmérő fölé írt Thalész-kör.
A példa állítása tehát a Thalész-tétel megfordításának következménye.
3. példa
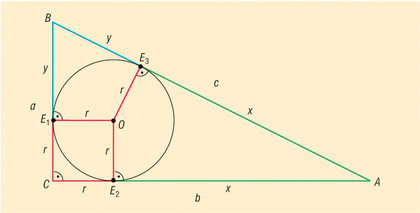
Bizonyítsuk be, hogy a derékszögű háromszögbe beírt kör átmérőjének hossza a két befogó hosszának összegénél az átfogó hosszával kisebb.
Megoldás
Az 1. példa megoldása során bebizonyítottuk, hogy a körhöz külső pontból húzott érintőszakaszok egyenlő hosszúak.
CE 1 = CE 2 = r ; E 2 A = AE 3 = x ; E 3 B = BE 1 = y .
A két befogó hosszának összege:
a + b = x + y + 2 r . (1)
Az átfogó hossza:
c = x + y . (2)(2)-t (1)-be helyettesítve kapjuk, hogy
2 r = a + b – ca + b = c + 2 r ,
és ezt akartuk bizonyítani.