Construct a Slope Triangle
Create the following construction of a slope triangle. Afterwards, use your construction in order to work on the following tasks.
Construction steps
| 1. | 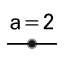 | Create two sliders for m and b. Hint: Use the default values for the slider interval of -5 to 5. |
| 2. | | Enter the equation of a line y = m*x + d into the Algebra Input and press the Enter key. |
| 3. |  | Create the intersection point of the line and the y-axis. Note: The name of the intersection point is A. |
| 4. |  | Create a line through point A that is parallel to the x-axis. |
| 5. |  | Create a point B on the parallel line. |
| 6. | 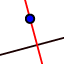 | Create a line through point B that is perpendicular to the x-axis. |
| 7. |  | Intersect these two new lines. Note: The name of the intersection point is C. |
| 8. | 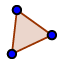 | Draw the slope triangle ABC. |
| 9. | | Change the names of the two legs of the slope triangle to Δy and Δx. |
| 10. | | Show Name & Value of the legs of the slope triangle by changing the Labeling setting on tab Basics of the Properties dialog. |
Tasks
Change the values of the sliders m and b, so that you can successively explore the following lines:
(1) y = 2x + 1
(2) y = 3x - 2
(3) y = -x + 2
Task 1:
For each of the lines above, move point B and write down the values of Δy and Δx for at least four different slope triangles.
Note: Two of your slope triangles should be on the right and two on the left side of the y-axis.
Task 2:
For each of your slope triangles, calculate the ratio of its two legs and compare the four resulting values for each line.