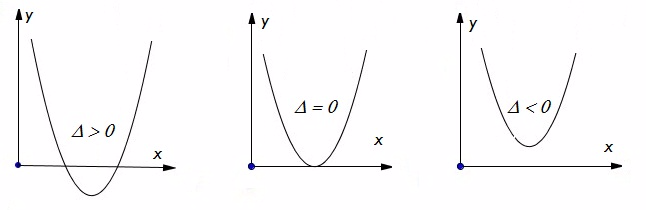
Como encontrar as raízes da Função Quadrática:

Autore:Lais Garda

Para:

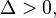a função terá duas raízes.
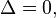a função terá uma raiz apenas (com maior precisão, diz-se que a função tem duas raízes iguais)
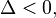não terá raíz (com maior precisão, diz-se que a função não tem raízes reais, tendo duas raízes complexos conjugados).

As duas raízes da função quadrática

onde

são

Essa fórmula é chamada de Fórmula Quadrática.

Dado
Se 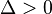, então existem duas raízes distintas uma vez que é um número real positivo.
Se 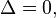então as duas raízes são iguais, uma vez que é igual a zero.
Se 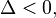então as duas raízes são números complexos conjugados, uma vez que é imaginário.

Exemplo: Dada a função 4x² –28x + 49 = 0 defina as raízes: Antes de resolver devemos retirar os coeficientes da equação: a = 4 b = – 28 c = 49 Agora, vamos calcular o valor de ∆. ∆ = b² – 4 . a . c(basta substituir os valores dos coeficientes) ∆ = (-28)² – 4 . 4 .49 ∆ = 784 – 784 ∆ = 0 (com o valor de ∆, basta substituir os valores dos coeficientes na fórmula) X = – b ± √ ∆ 2 . a X = – (-28) ±√0 2 . 4 X = 28 ± 0 8 X1= 28 + 0 = 28 = 3,5 8 8 X2 = 28 – 0 = 28 = 3,5 8 8 Portanto, as raízes encontradas foram 3,5 e 3,5 (duas raízes reais iguais)

Como encontrar as raízes da Função Quadrática:

Modelo de como são apresentados os gráficos com as raízes >, =, ou < de 0

Nuove risorse

Scopri le risorse

Scopri gli argomenti