Andere oplossingen
In 1939 vond Roland Sprague een oplossing met niet minder dan 55 verschillende vierkanten, waarvan het grootste als zijde 2320 had..
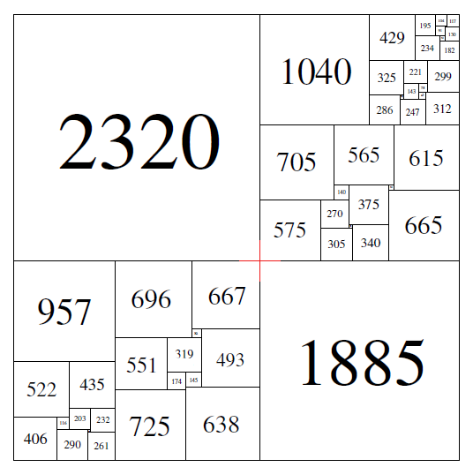
Nadat Tuttle, samen met andere wiskundigen het probleem in verband brachten met elektronische netwerken, vond men nog meer oplossingen. In 1962 toonde de Nederlandse informaticus Arie Duijvestijn aan dat het nooit met minder dan 21 zou kunnen. Wat het minimum echt was, dat wist hij nog niet, tot hij in 1978 effectief een oplossing met slechts 21 vierkanten vond. Het onderstaande applet toont zijn oplossing
Meer info
Veel meer informatie over de geschiedenis van het probleem, het verband met met elektronische netwerken enz. vind je op de website http://www.squaring.net/index.html