Google Classroom
GeoGebraTarefa
GeoGebra

Função logarítmica

Autor:Lucas Pereira de Andrade

O que é logaritmo?

Trata-se da operação que encontra o expoente de uma potência quando se conhece sua base e seu resultado, uma espécie de inverso da potenciação.

O que é função logarítmica?

O logaritmo de um número é definido como o expoente ao qual se deve elevar a base a para obter o número x, ou seja
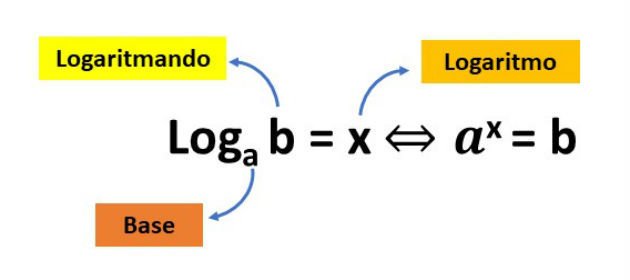
A função logarítmica de base a é definida como f (x) = loga x, com areal, positivo e a ≠ 1. A função inversa da função logarítmica é a função exponencial

Exemplos

Propriedades da função logarítmica

1°Propriedade Quando não aparece a base de um logaritmo consideramos que seu valor é igual a 10

2° Propriedade

Logaritmo de um produto: Em qualquer base, o logaritmo do produto de dois ou mais números positivos é igual à soma dos logaritmos de cada um desses números. Exemplo Considerando e , determine o valor do. Solução Podemos escrever o número 60 como um produto de 2.3.10. Neste caso, podemos aplicar a propriedade para esse produto: Aplicando a propriedade do logaritmo de um produto: As bases são iguais a 10 e o  = 1. Substituindo esses valores, temos: = 0,3 + 0,48 + 1 = 1,78

3°Propriedade

Logaritmo de um quociente: Em qualquer base, o logaritmo do quociente de dois números reais e positivos é igual à diferença entre os logaritmos desses números. Exemplo: Considerando , determine o valor do . Solução Podemos escrever 0,5 como sendo 5 dividido por 10, neste caso, podemos aplicar a propriedade do logaritmo de um quociente.

4°Propriedade

Logaritmo de uma potência: Em qualquer base, o logaritmo de uma potência de base real e positiva é igual ao produto do expoente pelo logaritmo da base da potência. Podemos aplicar essa propriedade no logaritmo de uma raiz, pois, podemos escrever uma raiz na forma de expoente fracionário. Assim:Exemplo: Considerando , determine o valor do . Solução: Podemos escrever o número 81 como sendo 34. Neste caso, vamos aplicar a propriedade do logaritmo de uma potência, ou seja:

5°Propriedade

Mudança de base: Para aplicar as propriedades anteriores é necessário que todos os logaritmos da expressão estejam na mesma base. Do caso contrário, será necessário transformar todos para uma mesma base. A mudança de base também é muito útil quando precisamos usar a calculadora para encontrar o valor de um logaritmo que está em uma base diferente de 10 e de e (base neperiana). A mudança de base é feita aplicando-se a seguinte relação: Uma aplicação importante dessa propriedade é que o log ab é igual ao inverso do log ba, ou seja: Exemplo: Escreva o na base 10. Solução: Vamos aplicar a relação para mudar o logaritmo para a base 10:

Um vídeo brabo para ajudar.

Gráfico de uma função logarítmica

Para a construção do gráfico da função logarítmica devemos estar atentos a duas situações: a > 1 0 < a < 1

Para a > 1, temos o gráfico da seguinte forma: (crescente)

Para 0 < a < 1, temos o gráfico da seguinte forma: (decrescente)

Características do gráfico da função logarítmica y = logax

O gráfico está totalmente à direita do eixo y, pois ela é definida para x > 0. Intersecta o eixo das abscissas no ponto (1,0), então a raiz da função é x = 1. Note que y assume todos as soluções reais, por isso dizemos que a Im(imagem) = R. Através dos estudos das funções logarítmicas, chegamos à conclusão de que ela é uma função inversa da exponencial. Observe o gráfico comparativo a seguir: Podemos notar que (x,y) está no gráfico da função logarítmica se o seu inverso (y,x) está na função exponencial de mesma base.

Vídeo brabo sobre a função logarítmica.

Questões

1) (PUC/SP - 2018) As funções , com k um número real, se intersectam no ponto   . O valor de g(f(11)) é:

Assinale a sua resposta aqui
  • A
  • B
  • C
  • D
Verifique minha resposta (3)

2) (UFRGS - 2018) Se  + = 1, então o valor de x é

Assinale a sua resposta aqui
  • A
  • B
  • C
  • D
  • E
Verifique minha resposta (3)

3) O valor do imposto pago por uma certa empresa, com em milhares, em função do tempo, ocorre segundo a função . Determine o valor do imposto pago daqui a 4 anos e o tempo no qual o imposto pago é 6 mil.

Verifique sua resposta

4) (PUC) Assinale a propriedade válida sempre:

Assinale a sua resposta aqui
  • A
  • B
  • C
  • D
  • E
Verifique minha resposta (3)

5) (Unesp) A expectativa de vida em anos em uma região, de uma pessoa que nasceu a partir de 1900 no ano () é dada por . Considerando que , uma pessoa dessa região que nasceu no ano 2000 tem expectativa de viver:

Assinale a sua resposta aqui
  • A
  • B
  • C
  • D
  • E
Verifique minha resposta (3)

6) Os valores de x que satisfazem log x + log (x – 5) = log 36 são:

Assinale a sua resposta aqui
  • A
  • B
  • C
  • D
  • E
Verifique minha resposta (3)

Respostas:

1) Como as funções f(x) e g(x) se interceptam no ponto (2, ), então para encontrar o valor da constante k, podemos substituir esses valores na função g(x). Assim, temos: Então depois é apenas fazer a equação de , e por final colocar os resultados na equação g(f(11))
2) Temos a soma de dois logaritmos que apresentam bases diferentes. Então, para começar, vamos fazer uma mudança de base. Lembrando que para mudar a base de um logaritmo usamos a seguinte expressão: Alternativa: b) ∛9.
3)

Referencias

https://www.todamateria.com.br/funcao-logaritmica/ https://brasilescola.uol.com.br/matematica/funcao-logaritmica.htm https://www.todamateria.com.br/propriedades-dos-logaritmos/ https://brasilescola.uol.com.br/o-que-e/matematica/o-que-e-logaritmo.htm https://www.todamateria.com.br/logaritmo-exercicios/ https://www.respondeai.com.br/workspace/topico/13/976/exercicio/3351 https://www.coladaweb.com/exercicios-resolvidos/exercicios-resolvidos-de-matematica/funcao-logaritmica-e-exponencial

Novos Materiais

Descobrir recursos

Explorar Tópicos