Übung 1
Optimierung einer Getränkedose
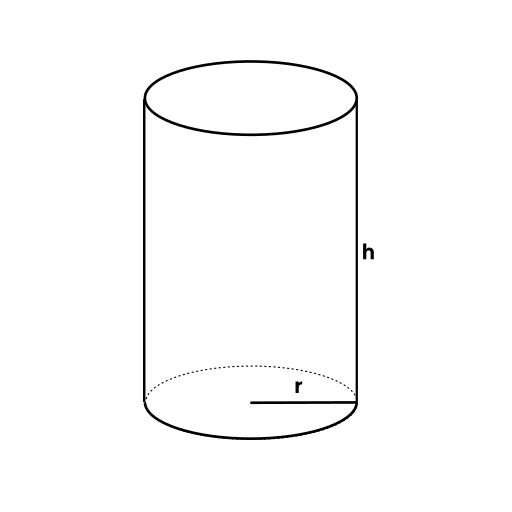
Du bist auf der Suche nach der optimalen Form für ihre Getränkedosen, um Materialkosten zu minimieren. Deine Aufgabe ist es, die Abmessungen für eine Dose zu finden, die genau einen Liter (1000 cm³) Flüssigkeit aufnehmen kann, aber gleichzeitig die Oberfläche möglichst klein hält. Die Dose soll die Form eines Zylinders haben.
1.Formuliere eine Gleichung für die Oberfläche A der Dose in Abhängigkeit von r ( Durchmesser ) und h ( Höhe).
2.Formuliere eine Gleichung für das Volumen ( 1 Liter ) und löse diese nach h auf.
3.Setzte nun die Gleichung für h in die Gleichung für die Oberfläche ein.
4.Setzte die ganze Formel in den Grafikrechner ein
Wenn du nun auf die 3 Punkte an der Funktion gehst, und dann auf spezielle Punkte, kannst du bei B den Punkt ablesen
Wie groß muss r sein, damit damit die Oberfläche kleinstmöglich ist ?