Google Classroom
GeoGebraGeoGebra Classroom
GeoGebra

Satz des Thales

Autor:JHäring
Thema:Geometrie
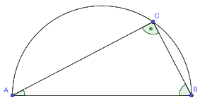
Image

Thema des Arbeitsblattes

In diesem Arbeitsblatt entdecken wir den Satz des Thales, eine bekannte Aussage in der Geometrie.

Arbeitsauftrag

Führe die Schritte 1 - 6 in der folgenden Konstruktionsanleitung im GeoGebra-Applet (unten) durch.

Konstruktionsanleitung

1. Schritt: Zeichne eine Strecke zwischen den Punkten und :
  • Klicke auf das Werkzeug Strecke Toolbar Imageund anschließend auf zwei Punkte.
2. Schritt: Zeichne einen weiteren Punkt in das GeoGebra-Applet ein:
  • Klicke auf das Werkzeug Punkt Toolbar Imageund anschließend in die weiße Zeichenfläche im GeoGebra-Applet.
3. Schritt: Zeichne eine Strecke zwischen den Punkten und und den Punkten und :
  • Klicke auf das Werkzeug Strecke Toolbar Imageund anschließend auf zwei Punkte.
4. Schritt: Zeichne die Winkel , und ein:
  • Klicke auf das Werkzeug Winkel Toolbar Image.
  • zeichnen: Klicke auf den Punkt , dann auf und zuletzt auf .
  • zeichnen: Klicke auf den Punkt , dann auf und zuletzt auf .
  • zeichnen: Klicke auf den Punkt , dann auf und zuletzt auf .
5. Schritt: Ändere die Darstellung der eingezeichneten Winkel:
  • Klicke auf das Werkzeug Bewege Toolbar Image.
  • Klicke auf einen Winkel und anschließend auf die Gestaltungsleiste rechts oben.
  • Klicke auf das Zahnrad, danach auf Darstellung, um den Winkel z.B. größer darzustellen.
6. Schritt: Zeichne einen Halbkreis, der die Punkte und enthält.
  • Klicke auf das Werkzeug Halbkreis Toolbar Image und anschließend auf zwei Punkte.

GeoGebra-Applet

Behauptung aufstellen

Klicke auf das Werkzeug Bewege Toolbar Image und verschiebe den Punkt im GeoGebra-Applet (oben). Was fällt dir auf, wenn der Punkt auf dem Halbkreis liegt? Formuliere einen Satz, der deine Beobachtung beschreibt. Folgende Formulierung könnte dabei hilfreich sein: Wenn der Punkt ... , dann ...

Antwort überprüfen
Im Folgenden wollen wir die soeben aufgestellte Behauptung beweisen.

Arbeitsauftrag

Führe die Schritte 7 - 10 in der folgenden Konstruktionsanleitung im GeoGebra-Applet (oben) durch:

Konstruktionsanleitung

7. Schritt: Binde den Punkt an den Halbkreis:
  • Klicke auf das Werkzeug Punkt anhängen / loslösen Toolbar Image.
  • Klicke auf den Punkt und anschließend auf den Halbkreis.
8. Schritt: Zeichne den Mittelpunkt zwischen den Punkten und ein:
  • Klicke auf das Werkzeug Mittelpunkt Toolbar Image und anschließend auf zwei Punkte.
9. Schritt: Bezeichne den soeben konstruierten Mittelpunkt mit .
  • Klicke auf das Werkzeug Bewege Toolbar Image und anschließend mit rechts auf den Mittelpunkt.
  • Klicke auf "Umbenennen".
10. Schritt: Zeichne eine Strecke zwischen und .
  • Klicke auf das Werkzeug Strecke Toolbar Image und anschließend auf zwei Punkte.

Gemeinsamkeiten der Dreiecke

Beantworte die folgende Frage mithilfe des GeoGebra-Applets (oben). Die Dreiecke und haben Gemeinsamkeiten. Es sind beides immer ...

Wähle alle richtigen Antworten aus
  • A
  • B
  • C
Antwort überprüfen (3)

Begründung der vorigen Aufgabe

Begründe deine Antwort aus der vorigen Aufgabe ohne Zuhilfenahme des GeoGebra-Applets (oben). Tipp: Betrachte die Länge der Strecken , und . Was fällt dir auf?

Antwort überprüfen
Wir wissen nun, dass gilt. Es bleibt allerdings immer noch zu zeigen, dass dies wirklich immer ein rechter Winkel sein muss.

Innenwinkelsumme

Beantworte die folgende Frage. Die Summe aller Innenwinkel in einem beliebigen Dreieck beträgt immer ...

Wähle alle richtigen Antworten aus
  • A
  • B
  • C
  • D
Antwort überprüfen (3)

Innenwinkelsumme

Beantworte die folgende Frage mithilfe des GeoGebra-Applets (unten). Die Summe aller Innenwinkel des Dreiecks ist ...

Wähle alle richtigen Antworten aus
  • A
  • B
  • C
  • D
Antwort überprüfen (3)

GeoGebra-Applet

Beweis abschließen

Folgere mithilfe der Antworten aus Aufgabe 5 und 6 deine Behauptung. Tipp: Gleichsetzten

Antwort überprüfen

Neue Materialien

Entdecke Materialien

Entdecke weitere Themen