Examples
Holder's Inequality is a fundamental result in mathematical analysis that establishes a relationship between the norms of two functions and their product. It is a generalization of the Cauchy-Schwarz Inequality and is widely used in various fields, including functional analysis and probability theory.
**Holder's Inequality:** Let (X, μ) be a measure space, and let f and g be measurable real-valued functions on X. For any two positive real numbers p and q such that 1/p + 1/q = 1, we have:
∫ |f(x) * g(x)| dμ ≤ ( ∫ |f(x)|^p dμ )^(1/p) * ( ∫ |g(x)|^q dμ )^(1/q)
In simpler terms, the absolute value of the integral of the product of two functions is bounded by the product of their respective p-norm and q-norm, where p and q are conjugate exponents (i.e., their reciprocals sum to 1).
**Examples:**
1. Holder's Inequality with p = 2 and q = 2 (Cauchy-Schwarz Inequality):
When p = 2 and q = 2, the exponents are conjugate, and Holder's Inequality reduces to the Cauchy-Schwarz Inequality.
Let's consider two functions f(x) = 3x and g(x) = √(x) on the interval [0, 1] with the Lebesgue measure. We can compute the integral of their product as follows:
∫ |f(x) * g(x)| dx = ∫ |3x * √(x)| dx
= ∫ 3x^(3/2) dx
= 3 * (2/5) * x^(5/2) | from 0 to 1
= 3 * (2/5) * 1^(5/2) - 3 * (2/5) * 0^(5/2)
= 3 * (2/5)
= 6/5
Now, let's compute the p-norm and q-norm of each function:
∫ |f(x)|^p dx = ∫ |3x|^2 dx = ∫ 9x^2 dx = 9 * (1/3) * x^3 | from 0 to 1 = 9 * (1/3) - 9 * (0/3) = 3
(∫ |f(x)|^p dx)^(1/p) = 3^(1/2) = √3
∫ |g(x)|^q dx = ∫ |√(x)|^2 dx = ∫ x dx = (1/2) * x^2 | from 0 to 1 = (1/2) - (0/2) = 1/2
(∫ |g(x)|^q dx)^(1/q) = (1/2)^(1/2) = √(1/2)
Now, applying Holder's Inequality with p = 2 and q = 2:
(6/5) ≤ (√3) * (√(1/2))
The result is valid, and we can see that it satisfies Holder's Inequality.
2. Holder's Inequality with Different Exponents:
Let's consider the functions f(x) = x^2 and g(x) = x^3 on the interval [0, 1] with the Lebesgue measure. This time, we will use p = 2 and q = 3, which are still conjugate exponents.
∫ |f(x) * g(x)| dx = ∫ |x^2 * x^3| dx = ∫ x^5 dx = (1/6) * x^6 | from 0 to 1 = (1/6) - (0/6) = 1/6
∫ |f(x)|^p dx = ∫ |x^2|^2 dx = ∫ x^4 dx = (1/5) * x^5 | from 0 to 1 = (1/5) - (0/5) = 1/5
(∫ |f(x)|^p dx)^(1/p) = (1/5)^(1/2) = √(1/5)
∫ |g(x)|^q dx = ∫ |x^3|^3 dx = ∫ x^9 dx = (1/10) * x^10 | from 0 to 1 = (1/10) - (0/10) = 1/10
(∫ |g(x)|^q dx)^(1/q) = (1/10)^(1/3) = ∛(1/10)
Now, applying Holder's Inequality with p = 2 and q = 3:
(1/6) ≤ (√(1/5)) * (∛(1/10))
Again, the inequality is satisfied.
These examples demonstrate the application of Holder's Inequality to compute upper bounds on the integral of the product of functions based on their individual norms. It allows us to relate integrals of products to norms and is a powerful tool in various areas of mathematics and analysis.
, 
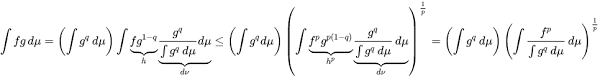
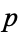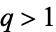. Then Hölder's inequality for integrals states that
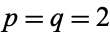, this inequality becomes Schwarz's inequality.Similarly, Hölder's inequality for sums states that
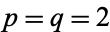, this becomes Cauchy's inequality.
