Ecuación cuadrática completa
La forma general de una ecuación de segundo grado es:
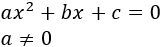Si b,c≠0, se dice que la ecuación es completa y sus soluciones las proporciona la fórmula
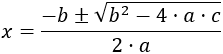
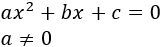Si b,c≠0, se dice que la ecuación es completa y sus soluciones las proporciona la fórmula
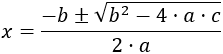
Ejemplo 1
Resolver la ecuación de segundo grado completa
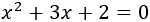Solución
Es una ecuación completa con coeficientes a=1, b=3y c=2. Aplicamos la fórmula:
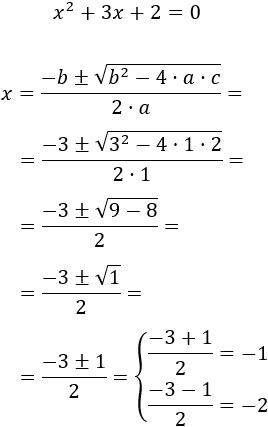Por tanto, las soluciones son -1 y -2.
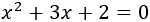Solución
Es una ecuación completa con coeficientes a=1, b=3y c=2. Aplicamos la fórmula:
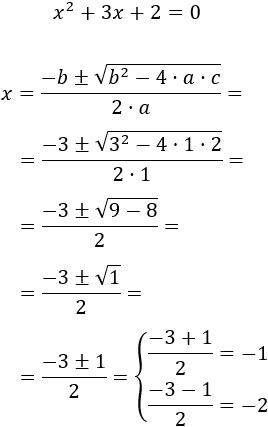Por tanto, las soluciones son -1 y -2.Más información:
- Ecuaciones de segundo grado resueltas
- Ecuaciones bicuadradas resueltas
- Fracciones equivalentes y fracción irreductible
- Potencias (propiedades y ejercicios)
- Teorema de Pitágoras (con problemas resueltos)
- Ecuaciones de primer grado explicadas
- Problemas resueltos de ecuaciones
- Sistemas de ecuaciones (métodos)
- Problemas resueltos de sistemas de ecuaciones
- Problemas de progresiones o sucesiones
- Problemas resueltos de mcm y mcd
- Problemas resueltos de trigonometría (seno, coseno y tangente)
- Problemas de movimiento rectilíneo uniforme (MRU)
- Ecuaciones exponenciales resueltas
- Integrales resueltas (directas, por sustitución y por partes)
- Números complejos o imaginarios
- Problemas y Ecuaciones
- Logaritmos
- Teorema de Pitágoras online
- Calculadoras de porcentajes online