A Center of IN-teresting Things

Fan of Harry Potter?

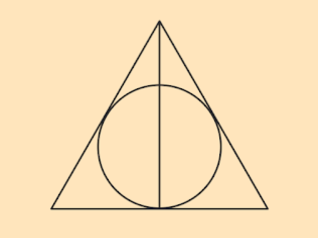
Do you recognize the symbol above?

This incircle is the symbol for the Dealthy Hallows, the namesake of the eighth book from the Harry Potter Series. The triangle represents the invisibility cloak, the vertical line is a magical wand, and the circle represents the ring with the resurrection stone fitted into it. Whoever possesses all three objects becomes the master of death.

Q1 - Don't Overthink It

One of the components for the Dealthy Hallows is an incircle, or an inscribed circle. 1. How would you define an inscribed circle? 2. Not all inscribed circles will be the same size? What factor(s) might affect this?

Our Problem

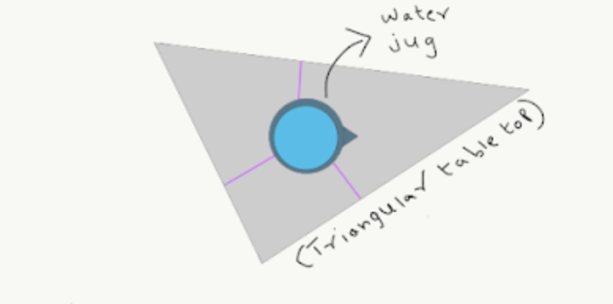
Imagine you work for a tavern (restaurant) in the magical universe of Harry Potter. You are required to prepare the table with silverware, napkins, plates, glasses, and a jug of water. Every table in the tavern is triangular and you want to place the water jug at the center of the table such that it is equally accessible to guests from all three sides (see the image below).

Let's Construct!

The location of the water jug marks the incenter of the triangular table. Use the following information to construct it. 1. Create angle bisectors for each angle of the triangle. a. Find the angle measure for each angle formed (there are six). 2. The intersection (point of concurrency) represents the incenter. 3. Create an inscribed circle that intersects each of the three points formed with the sides. (*Hint* - Try to "Circle Through Three Points" tool) 4. Construct a perpendicular line from the incenter to each side of the triangle. a. Measure the distance of each line constructed (there are three).

Construct the Incenter

Q2 - Drag the Vertices & Observe

What observations can you make about the construction of the incenter? What do you notice?

Q3 - Do the angle bisectors of a triangle's interior angles also bisect the sides opposite theses angles? *Hint: Use the Distance tool to help answer this question.*

Q4 - Is it ever possible for a triangle's incenter to lie outside the triangle? If so, under what conditions?

Q5 - Is it ever possible for a triangle's incenter to lie on the triangle itself? If so, under what conditions?

Q6 - Which statement(s) best describe the incenter?

Jelöld be válaszodat

A
equidistant from the sides of the triangle
B
intersection of perpendicular bisectors
C
intersection of altitudes
D
intersection of angle bisectors
E
intersection of medians
F
equidistant from the vertices of the triangle

Check my answer (3)

Q7 - Back to the Problem

Now that you have constructed the incenter, what information would you need to know in order to determine the exact location of the center of the triangular table in the tavern?