4.1 Solución de Un Problema de Función Cuadrática
Problema:
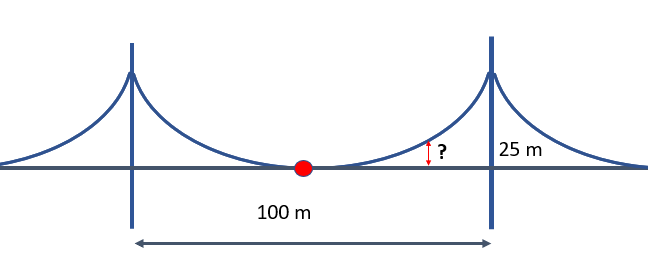
Los cables que sostienen un puente colgante forman un arco parabólico como se muestra en la figura.
Las torres que sostienen los cables están separados 100 m y tienen una altura de 25 m. Si los cables tocan la superficie del puente a la mitad de la distancia entre las torres.
Calcula la altura del cable a 10 m del centro del arco.
Solución
Sigue estas instrucciones para resolver el problema usando GeoGebra:
1. Crea un segmento de longitud 100 usando la herramienta: 
sobre el eje x
2. Selecciona la herramienta punto 
y crealo en la coordenada (0,25), llámalo E.
3. Crea el vértice V con la herramienta en la coordenada (50,0).
3. Usa la barra de entrada para crear el punto D, Utiliza el comando: D=(x(V)*2,y(E))
4. Crea dos segmentos 
que una al punto E con el Origen y el punto D con el punto (100,0)
Para poder resolver el problema dados los datos que tenemos, necesitamos encontrar la ecuación de la parábola sabiendo que conocemos el vértice y un punto dado.
La ecuación de una parábola vértical que cumple esas dos condiciones es:
Recuerda que el vértice se define como: y
Sustituyendo los datos que tenemos sobre la fórmula, tenemos:
Dado que el único valor que no conocemos es "p" ; podemos calcularlo automáticamente con Geogebra:
5. Utiliza la barra de entrada para calcularlo, digita:
¡Ya tenemos todo para graficar nuestra parábola!
6. Digita en la barra de entrada:
7. Ahora, crea un punto sobre el segmento que está en el eje "x" usando 
.
Esto lo hacemos con la finalidad de poder calcular el valor que nos piden, no solo a 10 m, sino en cualquier valor.
8. Crea una recta perpendicular 
seleccionando el punto que acabas de crear y el eje "x"
9. Ubica la intersección de la parábola y la recta creada usando 
.
10. Esconde la intersección y la recta, y crea un segmento con líneas punteadas para ubicar su medida, asegúrate de que se muestre en la etiqueta su nombre y su valor.
Asegúrate dar formato a tu escena para que esta luzca lo mejor posible.
¡Ahora ya puedes calcular la distancia del piso a la cuerda del puente desde cualquier distancia!
sobre el eje x
2. Selecciona la herramienta punto y crealo en la coordenada (0,25), llámalo E.
3. Crea el vértice V con la herramienta en la coordenada (50,0).
3. Usa la barra de entrada para crear el punto D, Utiliza el comando: D=(x(V)*2,y(E))
4. Crea dos segmentos que una al punto E con el Origen y el punto D con el punto (100,0)
Para poder resolver el problema dados los datos que tenemos, necesitamos encontrar la ecuación de la parábola sabiendo que conocemos el vértice y un punto dado.
La ecuación de una parábola vértical que cumple esas dos condiciones es:
Recuerda que el vértice se define como: y
Sustituyendo los datos que tenemos sobre la fórmula, tenemos:
Dado que el único valor que no conocemos es "p" ; podemos calcularlo automáticamente con Geogebra:
5. Utiliza la barra de entrada para calcularlo, digita:
¡Ya tenemos todo para graficar nuestra parábola!
6. Digita en la barra de entrada:
7. Ahora, crea un punto sobre el segmento que está en el eje "x" usando .
Esto lo hacemos con la finalidad de poder calcular el valor que nos piden, no solo a 10 m, sino en cualquier valor.
8. Crea una recta perpendicular seleccionando el punto que acabas de crear y el eje "x"
9. Ubica la intersección de la parábola y la recta creada usando .
10. Esconde la intersección y la recta, y crea un segmento con líneas punteadas para ubicar su medida, asegúrate de que se muestre en la etiqueta su nombre y su valor.
Asegúrate dar formato a tu escena para que esta luzca lo mejor posible.
¡Ahora ya puedes calcular la distancia del piso a la cuerda del puente desde cualquier distancia!