Von der Potenzfunktion zur ganzrationalen Funktion
In der allgemeinen Form sieht eine Potenzfunktion wie folgt aus: mit und. Den Einfluss des Parameters a kannst du mit dem folgendem Applet untersuchen.
Verschiebe den Schieberegler und beantworte mit Hilfe deiner Beobachtungen die Fragen.
Der Parameter a ...
Für gerade n:
Umso größer der Parameter a, ...
Diese Beobachtung gilt auch für ungerade n, allerdings passt hier der Begriff "Öffnung" nicht so recht.
Hat das a ein negatives Vorzeichen, so ...
Das folgende Diagramm stellt zum einen den Graphen von (gestrichelt) dar. Der andere Graph gehört zum Funktionsterm . Gib das Intervall an, in dem a liegen muss.
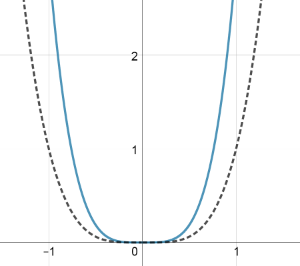
Überlagerung mehrerer Potenzfunktionen
Natürlich können wir nun auch mehrere Potenzfunktionen nehmen und diese addieren.
z.B. und
Erkläre, wie der Graph von g aus den beiden anderen Graphen hervorgeht.
Diese Prinzip lässt sich beliebig erweitern. Man spricht dann von einer ganzrationalen Funktion
vom Grad n (höchster Exponent).
Als Beispiel kannst du hier mal mit einer ganzrationalen Funktion vom Grad 4 herumspielen und die Koeffizienten () einstellen.
Fülle nun das Arbeitsblatt aus.