Umkreis eines Dreiecks
Aufgabenstellung
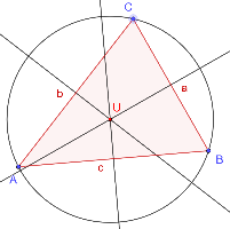
Konstruktionsanleitung
| 1 |  | Konstruiere das Dreieck ABC: Klicke auf das Werkzeug Vieleck und lege die Eckpunkte des Dreiecks in der Aufgabenstellung fest. |
| 2 |  | Zeige die Beschriftung der Punkte A,B,C und der Seiten a,b,c an: Klicke auf das Werkzeug Bewege und anschließend mit rechts auf das entsprechende Objekt um die Beschriftung anzeigen zu lassen. |
| 3 |  | Erzeuge die drei Mittelsenkrechten des Dreiecks: Klicke auf das Werkzeug Mittelsenkrechte und anschließend auf zwei Punkte, um die Mittelsenkrechte zwischen diesen beiden Punkten zu erzeugen. |
| 4 |  | Stelle die Mittelsenkrechten gestrichelt dar: Klicke auf das Werkzeug Bewege und anschließend mit links auf das entsprechende Objekt. Klicke auf die Gestaltungsleiste rechts oben und ändere die Darstellung des Objekts. |
| 5 |  | Beschrifte die Mittelsenkrechten mit ma, mb, mc : Klicke auf das Werkzeug Bewege und anschließend mit rechts auf das entsprechende Objekt um es umzubenennen. Um ma zu schreiben, stelle einen Unterstrich voran, etwa m_a. |
| 6 |  | Erzeuge den Umkreismittelpunkt des Dreiecks: Klicke auf das Werkzeug Schnittpunkt und anschließend auf zwei der soeben konstruierten Mittelsenkrechten. |
| 7 |  | Konstruiere den Umkreis des Dreiecks: Klicke auf das Werkzeug Kreis mit Mittelpunkt durch Punkt und anschließend auf den soeben erzeugten Umkreismittelpunkt. Klicke danach auf einen der drei Eckpunkte des Dreiecks. |
Verständnisaufgaben bzw. -fragen
Entscheide, ob die folgende Aussage wahr oder falsch ist: Jedes Dreieck besitzt genau einen Umkreis.
Entscheide, ob die folgende Aussage wahr oder falsch ist: Die drei Mittelsenkrechten des Dreiecks schneiden sich immer in genau einem Punkt.
Für welche Koordinaten der Punkte A,B und C liegt der Umkreismittelpunkt genau im Koordinatenursprung ?
Entscheide, ob die folgende Aussage wahr oder falsch ist: Der Umkreismittelpunkt liegt immer innerhalb des Dreiecks
Welches Problem entsteht, wenn die Punkte A,B und C die Koordinaten , und haben? Formuliere deine Beobachtung in einem Freitext.
Entscheide, ob die folgende Aussage wahr oder falsch ist: Ist das Dreieck ABC rechtwinklig, so ist der Mittelpunkt der Hypothenuse des Dreiecks zugleich der Umkreismittelpunkt.
Welche Eigenschaft des Dreiecks ABC muss erfüllt sein, damit der Umkreismittelpunkt innerhalb bzw. außerhalb des Dreiecks liegt? Formuliere zwei Merksätze. Folgende Formulierungen könnten dabei hilfreich sein: Der Umkreismittelpunkt befindet sich innerhalb des Dreiecks, wenn ... Der Umkreismittelpunkt befindet sich außerhalb des Dreiecks, wenn ...