Google Classroom
GeoGebraTarefa
GeoGebra

Lei dos cossenos

Autor:Reinaldo Santos
Image

Contextualizando

É muito comum que nas zonas rurais existam estradas de terras ligando propriedades rurais. Imagine que uma fazenda (ponto A) está ligada à rodovia mais próxima por duas estradas. A primeira estrada possui 4km de extensão, já a segunda tem 6km de extensão, como mostra a figura abaixo:

A primeira estrada e a segunda são retas e formam um ângulo de 60°. Qual a distância entre os pontos B e C da rodovia?

Note que o triângulo acima não é retângulo, logo o teorema de Pitágoras não é aplicável nesse caso. Então, o que deve ser feito?

A lei dos cossenos

É para casos como esse que existe a lei dos cossenos, veja o triângulo abaixo:

Segundo a lei, podemos utilizar as seguintes relações: 1- a²= b²+c² -2.b.c.cos α 2- b²= a²+c² -2.a.c.cos β 3- c²=a²+b² -2.a.b.cos γ

Vamos então resolver a problemática da fazenda. Precisamos saber a medida de BC, porém não sabemos qual é, logo vamos chama-la de "x". Ok, vamos aplicar a fórmula!

x² = 4² + 6² - 2.4.6.cos 60° (em outras palavras x é igual a soma do quadrado dos dois outros lados menos duas vezes o produto dos outros lados vezes o cosseno do ângulo oposto ao "x"/lado BC)

x² =16 + 36 -48. 1/2 x² =52 - 24 x =28 x =4.7 x =27 Logo, a distância de BC é de 27 Km

Ativadades

Agora resolveremos algumas atividades

Questão 1

Questão 1
Resolução
O comprimento do muro necessário para cercar o terreno é igual ao seu perímetro. Para esse cálculo, basta somar os comprimentos do lado do triângulo. 10 + 15 + x O valor de x pode ser encontrado por meio da lei dos cossenos: x2 = 102 + 152 – 2·10·15·cos60° x2 = 100 + 225 – 2·150·cos60° x2 = 325 – 300·1/2 x2 = 325 – 150 x2 = 175 x = √175 x = √[5·35] x = √[5·5·7] x = √[52·7] x = 5√7 Logo, a soma que representa o perímetro desse triângulo é: 10 + 15 + x 25 + 5√7 5·5 + 5√7 5(5 + √7)

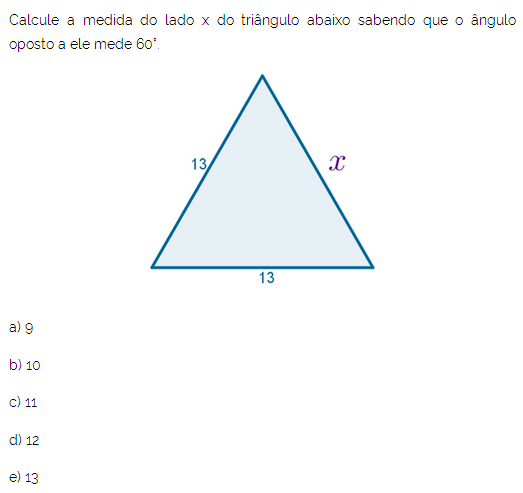
Questão 2

Questão 2
Resolução A partir da lei dos cossenos, dada pela fórmula abaixo, teremos: x2 = a2 + b2 – 2·a·b·cosα Sabendo que o ângulo oposto a x mede 60° e que as medidas de a e b são 13, teremos: x2 = 132 + 132 – 2·13·13·cos60 x2 = 169 + 169 – 2·13·13·cos60 x2 = 169 + 169 – 2·169·1/2 Colocando 169 em evidência: x2 = 169(1 + 1 – 2·1/2) x2 = 169(1 + 1 – 1) x2 = 169(1) x2 = 169 x = √169 x = 13 Outra forma de resolver esse problema: sabendo que um triângulo equilátero possui todos os lados e ângulos iguais e que seus ângulos são iguais a 60°, é possível mostrar pelo caso LAL que o triângulo do exercício é congruente a um triângulo equilátero de lado 13. Logo, o último lado também mede 13.

Questão 3

Considere um triângulo que possui dois lados de medidas 10 e 12 cm. O encontro desses lados forma um ângulo de 60°. Qual é o valor da medida do terceiro lado do triângulo? Para iniciar a resolução desse problema, vamos fazer um esboço do triângulo descrito:

Resolução

Seja a = 12, b = x, c = 10  , = 60°, aplicando a lei dos cossenos, teremos: b² = c² + a² – 2ac.cos  x² = 10² + 12² – 2.12.10.cos 60° x² = 100 + 144 – 240.½ x² = 244 – 120 x² = 124 x = √124 x = 2√31 cm x ≈ 11,13 cm Portanto, o terceiro lado do triângulo mede aproximadamente 11,13 cm.

Novos Materiais

Descobrir recursos

Explorar Tópicos