OBMEP - Nível 2
2013 - Questão 11
Considere um retângulo ABCD onde o comprimento dos lados são AB=4 e BC=8. Sobre os lados BC e AD se fixam os pontos M e N, respectivamente, de modo que o quadrilátero BMDN seja um losango. Calcule a área deste losango.
Compreendendo o problema...
Para resolver uma questão como esta, é importante visualizar o enunciado. Vamos ver, a seguir, o que acontece.
Temos um retângulo ABCD em que precisamos, primeiro determinar a localização correta dos pontos M e N de modo a obter o losango BMDN.
Para isso, movimente o ponto M, buscando fazer com que o polígono lilás seja um losango.
Marque a caixinha das diagonais para visualizar melhor. Quando terminar, marque a caixinha para exibir o losango e verifique se você conseguiu encontrar o polígono correto.
O que acontece com as diagonais quando você encontra o lugar exato para o ponto M?
Fácil, fácil...
Agora que já compreendemos o enunciado, precisamos traçar um percurso para determinar a medida da área deste losango.
Bem, mas como um losango é um tipo específico de paralelogramo, podemos determinar a área desta figura usando a mesma estratégia que usamos quando calculamos a área de um paralelogramo, ou seja, devemos determinar o resultado da multiplicação entre a medida da base e a medida de sua altura.
Agora ficou bem mais fácil! Repare que a medida da altura deste paralelogramo é igual a 4. Agora só nos resta determinar a medida de sua base. Vamos considerar que esta medida que precisamos determinar seja representada por "x".
Veja o que acontece e responda as perguntas a seguir.
Qual é o valor da medida da altura do paralelogramo?
Agora só nos resta determinar a medida de sua base. Vamos considerar que esta medida que precisamos determinar seja representada por "x".
Repare que, como estamos falando de um losango, esta medida é igual ao lado maior do triângulo retângulo formado pelos vértices AMB.
Para determinar este valor desconhecido é necessário usar uma propriedade comum a todos os triângulos retângulos. Veja o que acontece quando construímos quadrados cujos lados tenham as mesmas medidas dos lados do triângulo retângulo AMB.
Mova o vértice vermelho para baixo e o vértice laranja para a esquerda até onde for possível e responda as perguntas a seguir.
Repare o que acontece com esses quadriláteros que movemos.
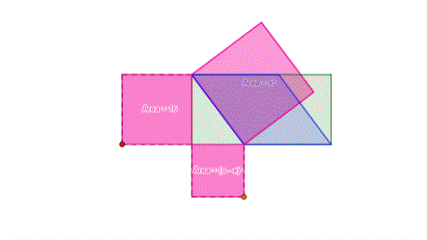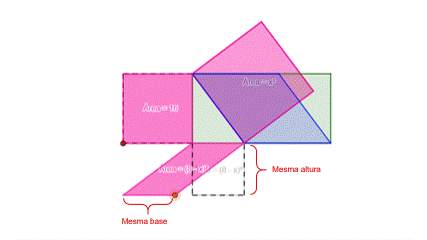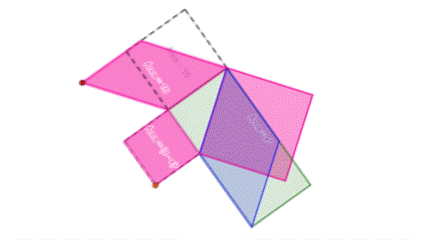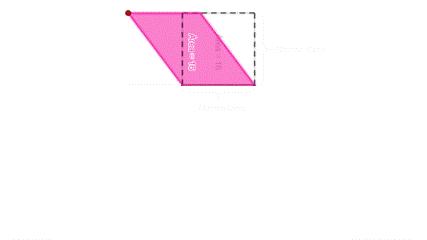
São equivalentes!
Repare que os paralelogramos que encontramos movendo os vértices dos quadrados possuem as mesmas medidas de área e altura de antes.
O que podemos concluir com essa informação?
Continuando...
Na tela a seguir, movimente o vértice para modificar o polígono encontrado novamente.
Mova os vértices azul e verde para ver o que acontece.
Continuam equivalentes!
Novamente, temos paralelogramos sendo transformados em outros paralelogramos. Neste caso em específico, obtivemos retângulos que possuem a mesma base e a mesma altura dos paralelogramos anteriores e, por isso, permanecem tendo a mesma área, ou seja, possuem a área dos quadrados que tínhamos anteriormente.
A partir dessas informações, o que podemos concluir?
Teorema de Pitágoras
É exatamente o que o Teorema de Pitágoras nos diz quando afirma que "a soma dos quadrados dos catetos é igual ao quadrado da hipotenusa".
Repare que os quadrados menores foram obtidos a partir dos lados que formam o ângulo reto e, por isso, são chamados de catetos. Por outro lado, o quadrado maior é construído a partir do lado oposto ao ângulo reto e, por isso, recebe o nome de hipotenusa.
Seguindo adiante...
Pronto! Agora que já sabemos dessa propriedade, podemos usar essa informação para montar uma equação e determinar o valor desconhecido.
Voltando ao nosso desenho inicial, temos que os quadrados dos lados menores possuem área igual à 4² e (8 - x)² e o quadrado maior tem área igual à x². Veja como podemos resolver a equação:

Pronto!
Agora que sabemos a medida do comprimento do lado do losango, qual será a medida da sua área?
É isso!
Espero que tenham gostado.
Se você estiver com alguma dúvida, coloque sua pergunta no fórum.