Chaotic Self-Organizing Behavior in Low-Dimensional Lotka-Volterra Equations
Overview
Chaotic self-organizing behavior is an interesting phenomenon that can be seen in some instances of higher-dimensional Lotka-Volterra Equations. An excellent article on the conditions in which it occurs, and an example of such a system can be found here:
https://sprott.physics.wisc.edu/pubs/paper288.htm
We won't have a chance to study this topic in this course, however, to whet your appetite for this interesting area of study, the example of a 4 dimensional Lotka-Volterra System, and Figure 3 from the above article has been replicated in the downloadable .GGB (GeoGebra) file for you to explore. A screenshot of the file is below:
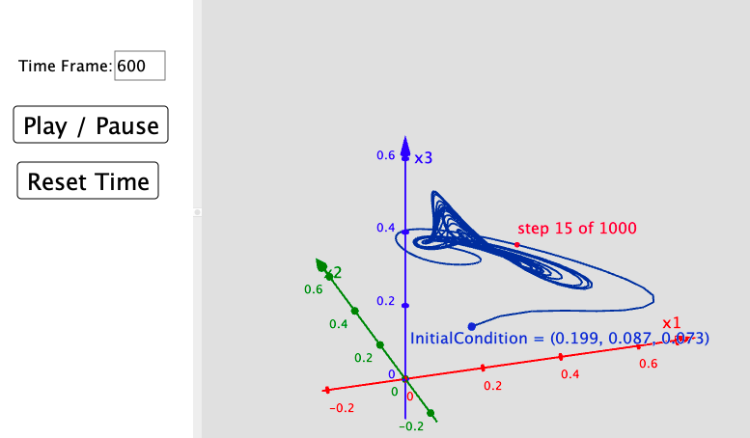
This is an animated GIF of the same file.
You can download the .GGB (GeoGebra) file here
https://cloudup.com/cH0HS72m6RB
You will need GeoGebra Classic 5 or 6 Desktop to open this file.
Note: The .GGB file may take up to 5 minutes to load on your computer, but once it's started it should work quickly. Also, after you wait for the initial launch, you may need to "jiggle"
InitialCondition to jump start the numerical ODE solver.
In the file you will find a 3-dimensional projection of the phase space perspective of the specific solutions of the 4-dimensional Lotka-Volterra System studied in the above article.
Chaotic self-organizing behavior can be observed in the file by adjusting the point InitialCondition. When you do so, observe that small changes in InitialCondition result in large differences in the specific solutions. Despite these large differences in the specific solutions, however, note that the solutions nonetheless exhibit self-organizing behavior oscillating around a certain point in the first octant.
If you REALLY want to try loading it in your web-browser, you can try doing so here: https://www.geogebra.org/m/sscerf4m But be warned, it may take a long time to load in browser.