Mantelfläche eines Rotationskörpers
Wieder eine scheibchenweise Herleitung
Der Umfang eines Kreises mit dem Radius ist . Der Mantel einer Kreisscheibe, also ein hohler Zylinder ohne Deckel mit der Höhe , hat die Fläche .
Einen Rotationskörper kann man nun aus lauter solchen Hohlzylindern zusammensetzen. Diese haben den Radius und als Höhe des Zylinders wird das Stück aus dem Funktionsgraphen eingesetzt (siehe Kapitel "Bogenlänge").
Daraus folgt für die Mantelfläche eines solchen schmalen Hohlzylinders: .
Um alle Hohlzylinder zur Mantelfläche aufzusummieren, verwendet man wieder ein Integral:
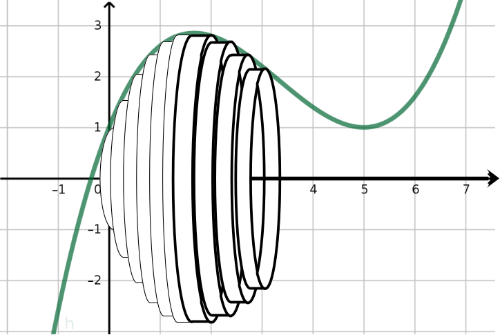
Mantefläche eines Rotationskörpers
Mit den
Beispielaufgabe
Die Funktionsgleichung der oben abgebildeten Funktion ist . Das mit den angedeuteten Hohlzylindern ausgefüllte Intervall ist .
Die Ableitungsfunktion von lautet:
Dann ist die Mantelfläche: