15. El lema de Yoneda
Esta actividad pertenece al libro de GeoGebra Música y Matemáticas.
El lema de Yoneda
Uno de los puntos cruciales en The Topos of Music es el lema de Yoneda. Este importante resultado viene a mostrar cómo podemos ampliar el conocimiento de una Categoría estableciendo una correspondencia entre sus objetos y las relaciones entre ellos.
Tras el lema de Yoneda hay un cambio de filosofía en el entendimiento de los núcleos de información. Ya no son los objetos los centros de atención, sino las diferentes perspectivas que podemos obtener de ellos. La comparación entre las distintas perspectivas de dos objetos nos ofrece, precisamente, la información deseada acerca del parecido o diferencia entre ambos objetos.
Los dos siguientes diagramas muestran un ejemplo intuitivo de este procedimiento. Aunque los motivos M1 y M2 son diferentes, podemos establecer una biyección entre las relaciones que mantienen ambos motivos (flechas) con otras notas fundamentales de la composición. La existencia de esta biyección nos indica que tales motivos pueden cumplir un papel similar en la composición, pero si hacemos solamente esto (sustituir cada motivo por sus relaciones) podemos llegar a la errónea conclusión de que ambos motivos son similares.
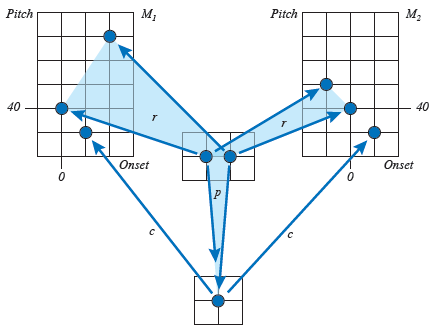
Sin embargo, si seguimos estudiando todas las perspectivas, es decir, todos los tipos de relación de ambos motivos entre sí y con los otros objetos, la diferente naturaleza de cada uno queda revelada.
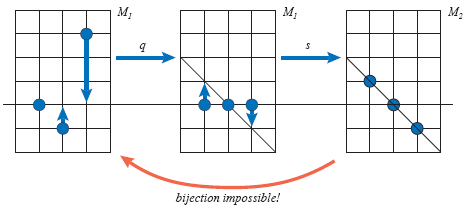
La composición de las proyecciones de M1 sobre la altura de la primera nota (q) y sobre la diagonal (s) da por resultado precisamente M2. Así que, intuitivamente, podemos ver a M2 como una transformación de M1. Pero esta transformación es irreversible. M1 “puede ver” a M2 pero M2 no “puede ver” a M1.
Un buen ejemplo de cómo el cambio de perspectiva ayuda al conocimiento lo tenemos en la pintura. La siguiente imagen muestra el famoso cuadro La escuela de Atenas, de Rafael.
Tomemos los elementos arquitectónicos esenciales, además de 58 figuras humanas, y simulemos en el espacio virtual del ordenador la estructura básica del cuadro:
Tomemos los elementos arquitectónicos esenciales, además de 58 figuras humanas, y simulemos en el espacio virtual del ordenador la estructura básica del cuadro:
Ahora rotamos el espacio virtual obteniendo una nueva perspectiva. Su análisis muestra simetrías que no podían encontrarse bajo la perspectiva del cuadro original.
